Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{n+1}{n-2}\)có giá trị nguyên
=> n+1\(⋮\)n-2=> n-2+3\(⋮\)n-2
=> 3\(⋮\)n-2=> n-2\(\in\){1,3,-1,-3}=>n\(\in\){3,5,1,-1}

Tìm tất cả các số tự nhiên n để :
a/ n^2 +12n là số nguyên tố
b/ 3^n +6 là số nguyên tố


Lời giải:
$n^2+12n=n(n+12)$ nên để $n^2+12n$ là số nguyên tố thì 1 trong 2 thừa số $n, n+12$ bằng $1$, số còn lại là số nguyên tố.
Mà $n< n+12$ nên $n=1$
Khi đó: $n^2+12n=1^2+12.1=13$ là số nguyên tố (thỏa mãn)

a) Để A là một phân số thì mẫu của \(A\ne0\) hay \(2n+3\ne0\)
\(\Leftrightarrow n\ne\dfrac{-3}{2}\)
b) Ta có : \(A=\dfrac{12n+1}{2n+3}\)
\(\Rightarrow A=\dfrac{12n+18-17}{2n+3}=\dfrac{12n+18}{2n+3}-\dfrac{17}{2n+3}\)
\(\Rightarrow A=\dfrac{6\left(2n+3\right)}{2n+3}-\dfrac{17}{2n+3}=6-\dfrac{17}{2n+3}\)
Để \(A\in Z\Leftrightarrow\dfrac{17}{2n+3}\in Z\)
\(\Leftrightarrow2n+3\in U\left(17\right)\)
mà \(U\left(17\right)=\left(1;-1;17;-17\right)\)
\(\Rightarrow n\in\left(-1;-2;7;-10\right)\)
Vậy \(A\in Z\Leftrightarrow n\in\left(-1;-2;7;-10\right)\)



Ta có:
Gọi A=n^2+12n=n.n+12n=(12+n).n
=> 12+n và n là ước của A
Vì A là 1 số nguyên tố nên A chỉ có 2 ước trong đó có 1 và cũng là 2 ước 12+n và n
=> 1 trong 2 ước 12+n và n bằng 1
12+n không thể bằng 1 vì n là số tự nhiên nên kết quả 12+n bé nhất là 12 (12+0)
=> n=1.
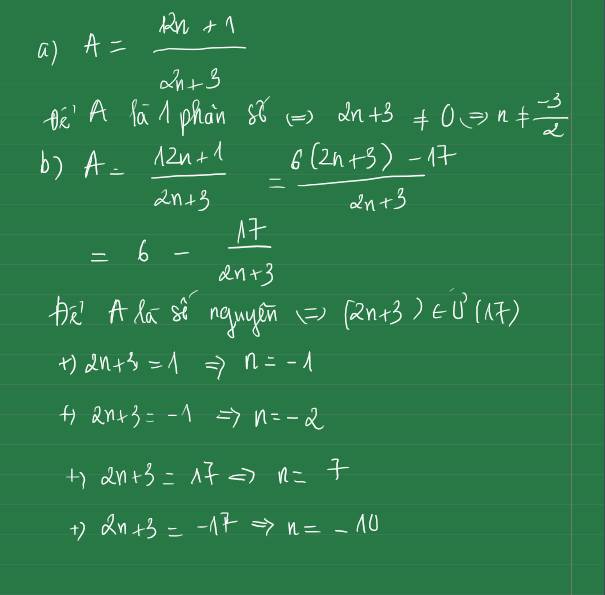
\(n^2+12n=n\left(n+12\right)\)
Để \(n^2+12n\)là số nguyên tố thì có một thừa số bằng 1
Mặt khác vì \(n< n+12\Rightarrow n=1\)
Vậy \(n=1\)
Thêm đk n thuộc N nha! Mình thử thôi,ko chắc đâu
Với n = 0 thì không phải là số nguyên tố
Với n= 1 => là số nguyên tố
Với n > 1 thì n2+12n = n(n+12) có nhiều hơn hai ước số nên là hợp số => loại
Vậy n = 1