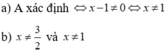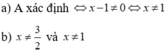
a)
A...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. \(P=\left(\frac{x-1}{x+3}+\frac{2}{x-3}+\frac{x^2+3}{9-x^2}\right):\left(\frac{2x-1}{2x+1}-1\right)\)\(\left(đkcđ:x\ne\pm3;x\ne-\frac{1}{2}\right)\) \(=\left(\frac{\left(x-1\right).\left(x-3\right)+2.\left(x+3\right)-\left(x^2+3\right)}{x^2-9}\right):\left(\frac{2x-1-\left(2x+1\right)}{2x+1}\right)\) \(=\frac{x^2-4x+3+2x+6-x^2-3}{x^2-9}:\frac{-2}{2x+1}\) \(=\frac{-2x-6}{x^2-9}.\frac{2x+1}{-2}\) \(=\frac{-2\left(x+3\right)}{\left(x-3\right).\left(x+3\right)}.\frac{2x+1}{-2}\) \(=\frac{2x+1}{x-3}\) b)\(\left|x+1\right|=\frac{1}{2}\Leftrightarrow\orbr{\begin{cases}x+1=\frac{1}{2}\\x+1=-\frac{1}{2}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{2}\left(koTMđkxđ\right)\\x=-\frac{3}{2}\left(TMđkxđ\right)\end{cases}}}\) thay \(x=-\frac{3}{2}\) vào P tâ đc: \(P=\frac{2x+1}{x-3}=\frac{2.\left(-\frac{3}{2}\right)+1}{-\frac{3}{2}-3}=\frac{4}{9}\) c)ta có:\(P=\frac{x}{2}\Leftrightarrow\frac{2x+1}{x-3}=\frac{x}{2}\) \(\Rightarrow2.\left(2x+1\right)=x.\left(x-3\right)\) \(\Leftrightarrow4x+2=x^2-3x\) \(\Leftrightarrow x^2-7x-2=0\) \(\Leftrightarrow x^2-2.\frac{7}{2}+\frac{49}{4}-\frac{57}{4}=0\) \(\Leftrightarrow\left(x-\frac{7}{2}\right)^2-\frac{57}{4}=0\) \(\Leftrightarrow\left(x-\frac{7}{2}-\frac{\sqrt{57}}{2}\right).\left(x-\frac{7}{2}+\frac{\sqrt{57}}{2}\right)\) bạn tự giải nốt nhé!! d)\(x\in Z;P\in Z\Leftrightarrow\frac{2x+1}{x-3}\in Z\Leftrightarrow\frac{2x-6+7}{x-3}=2+\frac{7}{x-3}\in Z\) \(2\in Z\Rightarrow\frac{7}{x-3}\in Z\Leftrightarrow x-3\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\) bạn tự làm nốt nhé a, \(\left(\dfrac{x^2-4x+3+2x+6-x^2-3}{\left(x+3\right)\left(x-3\right)}\right):\left(\dfrac{2x-1-2x-1}{2x+1}\right)\) \(=\dfrac{-2x+6}{\left(x+3\right)\left(x-3\right)}:\dfrac{-2}{2x+1}=\dfrac{-2\left(x-3\right)\left(2x+1\right)}{-2\left(x+3\right)\left(x-3\right)}=\dfrac{2x+1}{x+3}\) b, \(\left|x+1\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}-1\\x=-\dfrac{1}{2}-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\left(ktmđk\right)\\x=-\dfrac{3}{2}\end{matrix}\right.\) Thay x = -3/2 ta được \(\dfrac{2\left(-\dfrac{3}{2}\right)+1}{-\dfrac{3}{2}+3}=\dfrac{-2}{\dfrac{3}{2}}=-\dfrac{4}{3}\) a, ĐKXĐ : \(x-1\ne0\) => \(x\ne1\) TH1 : \(x-2\ge0\left(x\ge2\right)\) => \(\left|x-2\right|=x-2=1\) => \(x=3\left(TM\right)\) - Thay x = 3 vào biểu thức P ta được : \(P=\frac{3+2}{3-1}=\frac{5}{2}\) TH2 : \(x-2< 0\left(x< 2\right)\) => \(\left|x-2\right|=2-x=1\) => \(x=1\left(KTM\right)\) Vậy giá trị của P là \(\frac{5}{2}\) . a) \(P=\frac{x+2}{x-1}\) \(\left(ĐKXĐ:x\ne1\right)\) Ta có: \(\left|x-2\right|=1\text{⇔}\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\text{⇔}\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\) (loại x = 1 vì x ≠ 1) Thay \(x=3\) vào P, ta có: \(P=\frac{3+2}{3-2}=\frac{5}{1}=5\) Vậy P = 5 tại x = 3. b) \(Q=\frac{x-1}{x}+\frac{2x+1}{x^2+x}=\frac{x-1}{x}+\frac{2x+1}{x\left(x+1\right)}=\frac{x^2-1}{x\left(x+1\right)}+\frac{2x+1}{x\left(x+1\right)}\) (ĐKXĐ: x ≠ 0, x ≠ -1) \(=\frac{x^2+2x}{x\left(x+1\right)}=\frac{x\left(x+2\right)}{x\left(x+1\right)}=\frac{x+2}{x+1}\) a) ĐK: \(x\ne0,x\ne\pm3\) \(A=\left(\frac{x-3}{x^2-9}+\frac{1}{x+3}\right)\div\frac{x}{x+3}\) \(=\left(\frac{1}{x+3}+\frac{1}{x+3}\right)\div\frac{x}{x+3}\) \(=\frac{2}{x+3}\times\frac{x+3}{x}=\frac{2}{x}\) b) \(\left|A\right|=\left|\frac{2}{x}\right|=3\) \(\Leftrightarrow\orbr{\begin{cases}\frac{2}{x}=3\\\frac{2}{x}=-3\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{2}{3}\\x=-\frac{2}{3}\end{cases}}\)(thỏa mãn) Bài 1 : Với : \(x>0;x\ne1\) \(P=\left(1+\frac{1}{\sqrt{x}-1}\right)\frac{1}{x-\sqrt{x}}=\left(\frac{\sqrt{x}}{\sqrt{x}-1}\right).\sqrt{x}\left(\sqrt{x}-1\right)=x\) Thay vào ta được : \(P=x=25\) Bài 2 : a, Với \(x\ge0;x\ne1\) \(A=\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{2}{\sqrt{x}+1}-\frac{2}{x-1}=\frac{x+\sqrt{x}-2\sqrt{x}+2-2}{x-1}\) \(=\frac{x-\sqrt{x}}{x-1}=\frac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{\sqrt{x}}{\sqrt{x}+1}\) Thay x = 9 vào A ta được : \(\frac{3}{3+1}=\frac{3}{4}\) a xác định khi và chỉ khi x^2 -1 khác 0 suy ra x^2 khác 1 suy ra x khác 1 \(\frac{x^2-9}{x^2+2x+1}\)khác 0 suy ra x^2-9 khác 0 suy ra x^2 khác 9 suy ra x khác 3 1-x khác 0 suy ra x khác 1 vậy xác định khi x khác 1 và 3 b A = \(\frac{x+3}{x^2-1}\cdot\frac{x^2+2x+1}{x^2-9}-\frac{x}{1-x}\) = \(\frac{\left(x+3\right)\cdot\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)\left(x-3\right)\left(x+3\right)}-\frac{x}{1-x}\) = \(\frac{x+1}{\left(x-1\right)\left(x-3\right)}+\frac{x}{x-1}\) = \(\frac{x+1+x\left(x-3\right)}{\left(x-1\right)\left(x-3\right)}=\frac{x+1+x^2-3x}{\left(x-1\right)\left(x-3\right)}=\frac{x^2-2x+1}{\left(x-1\right)\left(x-3\right)}=\frac{\left(x-1\right)^2}{\left(x-1\right)\left(x-3\right)}=\frac{x-1}{x-3}\) a) \(ĐKXĐ:x\ne-3;x\ne2\) b) \(P=\frac{\left(x+2\right)\left(x-2\right)}{\left(x+3\right)\left(x-2\right)}-\frac{5}{\left(x-2\right)\left(x+3\right)}-\frac{x+3}{\left(x-2\right)\left(x+3\right)}\) \(P=\frac{x^2-4-5-x-3}{\left(x+3\right)\left(x-2\right)}\) \(P=\frac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}\) \(P=\frac{\left(x+3\right)\left(x-4\right)}{\left(x+3\right)\left(x-2\right)}\) vậy \(P=\frac{x-4}{x-2}\) \(P=\frac{-3}{4}\) \(\Leftrightarrow\frac{x-4}{x-2}=\frac{-3}{4}\) \(\Leftrightarrow4\left(x-4\right)=-3.\left(x-2\right)\) \(\Leftrightarrow4x-16=-3x+6\) \(\Leftrightarrow7x=22\) \(\Leftrightarrow x=\frac{22}{7}\) c) \(P\in Z\Leftrightarrow\frac{x-4}{x-2}\in Z\) \(\frac{x-2-6}{x-2}=1-\frac{6}{x-2}\in Z\) mà \(1\in Z\Rightarrow\left(x-2\right)\inƯ\left(6\right)\in\left(\pm1;\pm2;\pm3;\pm6\right)\) mà theo ĐKXĐ: \(\Rightarrow\in\left(\pm1;-2;3;\pm6\right)\) thay mấy cái kia vào rồi tìm \(x\) d) \(x^2-9=0\Rightarrow x^2=9\Rightarrow x=\pm3\) khi \(x=3\Rightarrow P=\frac{3-4}{3-2}=-1\) khi \(x=-3\Rightarrow P=\frac{-3-4}{-3-2}=\frac{-7}{-5}=\frac{7}{5}\)
K
Khách
CM
Cao Minh Tâm
19 tháng 4 2019
Đúng(0)
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 3 2022
9 tháng 3 2022
24 tháng 2 2020
JS
24 tháng 2 2020
DD
Đoàn Đức Hà
Giáo viên
16 tháng 7 2021
10 tháng 8 2021
10 tháng 8 2021
27 tháng 4 2018
27 tháng 4 2018
17 tháng 3 2019
