MT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 3 2022
Cho điểm M (2; -1) và đường thẳng Δ : x - y + 1 = 0 . Khi đó khoảng cách từ điểm M đến đường thẳng Δ bằng:
A. √22 B. 2√222 C. 1√212 D. 3√2
LH
1
30 tháng 1 2022
để M giao N là một khoảng thì \(\left[{}\begin{matrix}a>=-4\\a+3< =6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a>=-4\\a< =3\end{matrix}\right.\)
CM
28 tháng 2 2019
Đáp án A
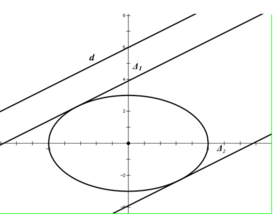
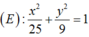có độ dài nửa trục lớn a = 5và độ dài nửa trục bé b= 3
Gọi 
là tiếp tuyến của (E) mà 
song song với d
=> x- 2y + C = 0.
Vì d tiếp xúc với (E) nên ta có:
Nên ta có hai tiếp tuyến của (E) song song với d là:
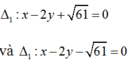
Vậy khoảng cách từ M đến đường thẳng d là lớn nhất là:
, khoảng cách từ M đến đường thẳng d là bé nhất là:
13 tháng 6 2022
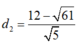
Bài 2:
a: \(x⋮5\)
mà 25<=x<=40
nên \(x\in\left\{25;30;35;40\right\}\)
b: \(6⋮x-1\)
\(\Leftrightarrow x-1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
hay \(x\in\left\{2;0;3;-1;4;-2;7;-5\right\}\)
Gọi \(M\left(m;0\right)\Rightarrow\overrightarrow{NM}=\left(m+28;-3\right)\)
\(\Rightarrow MN^2=\left(m+28\right)^2+9\)
\(MN=57\Leftrightarrow\left(m+28\right)^2+9=57^2\)
\(\Rightarrow\left[{}\begin{matrix}m=-28+18\sqrt{10}\\m=-28-18\sqrt{10}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}M\left(-28+18\sqrt{10};0\right)\\M\left(-28-18\sqrt{10};0\right)\end{matrix}\right.\)