K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BT
8 tháng 5 2017
a/ P(x)=2x3+2x2+x+5
Q(x)=x3-x2+x-1
b/ P(x)+Q(x)=2x3+2x2+x+5+x3-x2+x-1
P(x)+Q(x)=3x3+x2+2x+4
+/ P(x)-Q(x)=2x3+2x2+x+5-x3+x2-x+1
P(x)-Q(x)=x3+3x2+6
c/ Ta có: Q(1)=13-12+1-1=0 => x=1 là nghiệm của Q(x)
P(1)=2.13+2.12+1+5=10 khác 0 => x=1 không phải là nghiệm của P(x)
MM
8 tháng 5 2017
a) P(x) = 3x2+2x3+2x+5-x2-x
=2x3+3x2-x2-x+5
=2x3+2x2+x+5
Q(x) = x3-2x-2+3x-x2+1
=x3-x2-2x+3x-2+1
= x3-x2+x-1
KN
8 tháng 5 2017
a) \(P\left(x\right)=2x^2+2x^3+x\)
\(Q\left(x\right)=x^3+x-1-x^2\)
Sắp xếp theo lũy thừa giảm của biến ta có:
\(P\left(x\right)=2x^3+2x^2+x\)
\(Q\left(x\right)=x^3-x^2+x-1\)
b) \(P\left(x\right)+Q\left(x\right)=3x^3+x^2+2x-1\)
\(P\left(x\right)-Q\left(x\right)=x^3+3x^2+1\)
c) Thay x=1 vào đa thức Q(x), ta có:
\(Q\left(1\right)=1^3-1^2+1-1=0\)
Vậy x=1 là nghiệm của đa thức Q(x) (*)
Thay x=1 vào đa thức P(x), ta có:
\(P\left(1\right)=2.1^3+2.1^2+1=5\)
=> x=1 k phải là nghiệm của đa thức P(x) (**)
Từ (*) và (**) => (đpcm)
HN
2
PA
5 tháng 7 2016
a.
\(\frac{4^2\times4^3}{2^{10}}=\frac{4^2\times4^3}{2^{2\times5}}=\frac{4^2\times4^3}{\left(2^2\right)^5}=\frac{4^5}{4^5}=1\)
b.
\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\times3\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\right)^5\times3^5}{\left(0,2\right)^6}=\frac{243}{0,2}=1215\)
c.
\(\frac{2^7\times9^3}{6^5\times8^2}=\frac{2^7\times\left(3^2\right)^3}{\left(2\times3\right)^5\times\left(2^3\right)^2}=\frac{2^7\times3^6}{2^5\times3^5\times2^6}=\frac{3}{2^4}=\frac{3}{16}\)
d.
\(\frac{6^3+3\times6^2+3^3}{-13}=\frac{\left(2\times3\right)^3+3\times\left(3\times2\right)^2+3^3}{-13}=\frac{2^3\times3^3+3\times3^2\times2^2+3^3}{-13}=\frac{8\times3^3+3^3\times4+3^3}{-13}\)\(=\frac{3^3\times\left(8+4+1\right)}{-13}=\frac{27\times13}{-13}=-27\)
5 tháng 7 2016
a/ \(\frac{4^2.4^3}{2^{10}}=\frac{4^5}{2^{10}}=\frac{\left(2^5\right)^2}{2^{10}}=\frac{2^{10}}{2^{10}}=1\)
b/\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,6\right)^5}{\left(0,2\right)^5.\left(0,2\right)}=\left(\frac{0,6}{0,2}\right)^5.\frac{1}{\frac{1}{5}}=3^5.5=243.5=1215\)
c/ \(\frac{2^7.9^3}{6^5.8^2}=\frac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}=\frac{2^7.3^6}{2^5.3^5.2^6}=\frac{2^7.3.3^5}{2^7.2^4.3^5}=\frac{3}{16}\)
d/ \(\frac{6^3+3.6^2+3^3}{-13}=\frac{\left(2.3\right)^3+3.\left(2.3\right)^2+3^3}{-13}=\frac{2^3.3^3+3.2^2.3^2+3^3}{-13}=\frac{3^3.\left(2^3+2^2+1\right)}{-13}=\frac{27.13}{-13}=-27\)
23 tháng 10 2017
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a+b-c}{c}=\dfrac{a-b+c}{b}=\dfrac{-a+b+c}{a}=\dfrac{a+b-c+a-b+c-a+b+c}{a+b+c}=\dfrac{\left(a-a\right)+\left(b-b\right)+\left(c-c\right)+a+b+c}{a+b+c}=\dfrac{a+b+c}{a+b+c}=1\)
Hay \(\left\{{}\begin{matrix}a+b-c=c\\a-b+c=b\\b+c-a=a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=2c\\a+c=2b\\b+c=2a\end{matrix}\right.\)
Thay vào \(M\) ta có:
\(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{2c.2a.2b}{abc}=\dfrac{8abc}{abc}=8\)
2) Ta có:
\(3n+2-2n+2+3n-2n=\left(3n-2n+3n-2n\right)+\left(2+2\right)=2n+4⋮̸10\)
Đề sai
29 tháng 3 2020
Bạn ơi tính độ dài x j vậy bạn???
Chúc bạn hok tốt!!
Lần sau chép đủ đề nha!!
Nhãn
6 tháng 5 2020
Vậy đề bài và câu hỏi là gì thế?
TL: ko có câu hỏi nên ko thể làm!
~HOK TỐT~
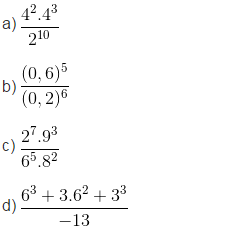
Tìm đa thức P biết: p+(x2-2y2+2 phần 3 xy)=-4x2+5y2+2 phần 3 xy