
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Ta có:
$A(x)=2x^3-7x^2-8x-4$
$=2x^2(x-2)-3x(x-2)-14(x-2)-32$
$=(x-2)(2x^2-3x-14)-32$
$=B(x)(2x^2-3x-14)-32$
Vậy đa thức thương là $2x^2-3x-14$

f: Ta có: \(\dfrac{4x^2-4xy+y^2}{y^2-4x^2}=\dfrac{A}{2x+y}\)
\(\Leftrightarrow\dfrac{A}{2x+y}=\dfrac{\left(2x-y\right)^2}{-\left(2x-y\right)\left(2x+y\right)}\)
\(\Leftrightarrow A=\dfrac{-\left(2x-y\right)^2\cdot\left(2x+y\right)}{\left(2x-y\right)\left(2x+y\right)}=-2x+y\)

Ban co the bi sai de nhe aban oi dung phai la x^2+ax-15 moi dung chu

\(P+R=-xy\cdot(x-y)\\\Leftrightarrow R=-xy(x-y)-P\\\Leftrightarrow R=-x^2y+xy^2-(5x^2y-2xy^2+xy-x+y-2)\\\Leftrightarrow R=-x^2y+xy^2-5x^2y+2xy^2-xy+x-y+2\\\Leftrightarrow R=(-x^2y-5x^2y)+(xy^2+2xy^2)-xy+x-y+2\\\Leftrightarrow R=-6x^2y+3xy^2-xy+x-y+2\)
Ta có:
\(P+R=-xy\cdot\left(x-y\right)\)
\(\Leftrightarrow\left(5x^2y-2xy^2+xy-x+y-2\right)+R=-x^2y+xy^2\)
\(\Leftrightarrow R=-x^2y+xy^2-5x^2y+2xy^2+xy+x-y+2\)
\(\Leftrightarrow R=\left(-x^2y-5x^2y\right)+\left(xy^2+2xy^2\right)+xy+x-y+2\)
\(\Leftrightarrow R=-6x^2y+3xy^2+xy+x-y+2\)



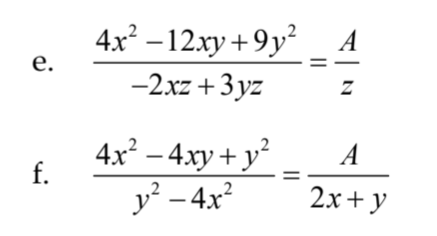
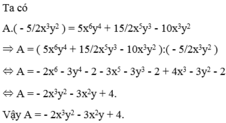
ta có :
\(A=\frac{\left(6+x\right)\left(36x-x^3\right)}{x^3+12x^2+36x}=\frac{x\left(x+6\right)^2\left(6-x\right)}{x\left(x+6\right)^2}=6-x\)