LS
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 8 2020
bài 2:
vì 4a12b chia hết cho cả 2 và 5 nên b=0
để 4a120 chia hết cho 9 thì 4+a+1+2+0 phải chia hết cho 9 => a=2
17 tháng 8 2020
bài 1:
a/ ta có : 18 = 2x9 => a là số chẵn và 7+3+a chia hết cho 9 => a=8
vậy a=8
b/ để 792a chia hết cho 3 và 5 => a=0 hoặc 5 và 7+9+2+a chia hết cho 3 => a=0
c/ để 87a chia hết cho 5 và 9 => a=0 hoặc a=5 và 8+7+a chia hết cho 9 => ko tìm được a thoả mãn
d/ a=5 và a=8
BH
29 tháng 12 2015
n + 3 chia hết choi n + 1
n + 1+ 2 chia hết cho n +1
2 chia hế cho n + 1
n + 1 thuộc U(2) = {-2 ; -1 ; 1 ; 2}
n + 1 = -2 =>? n = -3
n + 1= -1 => n = -2
n + 1 = 1 => n = 0
n + 1 = 2 => n = 1
OY
2
7 tháng 2 2020
để 1 số chia hết cho 8 thì ba chữ số tận cùng của nó phải chia hết cho 8 => a thuộc tập 2; 4; 6; 8
thử từng số vào để thỏa mãn chia hết cho 3 (tự làm) => 6 thỏa mãn
vậy a = 6
7 tháng 2 2020
Để \(\overline{aaaaa96}⋮8\)thì \(\overline{a96}⋮8\)
\(\Rightarrow a\in\left\{2;4;6;8\right\}\)
+) Nếu a=2 thì 2222296\(⋮̸\)3
\(\Rightarrow\)a=2 (loại)
+) Nếu a=4 thì 4444496\(⋮̸\)3
\(\Rightarrow\)a=4 (loại)
+) Nếu a=6 thì 6666696\(⋮\)3
\(\Rightarrow\)a=6 (thỏa mãn)
+) Nếu a=8 thì 8888896\(⋮̸\)3
\(\Rightarrow\)a=8 (loại)
Vậy a=6.
CM
4 tháng 1 2020
a) (b = 0; a = 4); (b = 2; a = 2);(b = 4; a = 0); (b = 4; a = 9).
b) (b = 0; a = 0); b= 0; a = 9); (b = 5; a = 4).
c) (b = 0; a= 7).
d) (b = 5; a = 2); (b = 5;a = 5); (b = 5;a = 8).
30 tháng 10 2023
Bài 4: Để tìm các chữ số a, b thỏa mãn các điều kiện, ta sẽ kiểm tra từng trường hợp.
a. Để số 4a12b chia hết cho 2, 5 và 9, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 2, nên b phải là số chẵn. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Vì số chia hết cho 9, nên tổng các chữ số trong số đó phải chia hết cho 9. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 4 + a + 1 + 2 + 0 = 7 + a. Để 7 + a chia hết cho 9, ta có a = 2.
- Nếu b = 5, thì tổng các chữ số là 4 + a + 1 + 2 + 5 = 12 + a. Để 12 + a chia hết cho 9, ta có a = 6.
Vậy, các giá trị thỏa mãn là a = 2 hoặc a = 6, và b = 0 hoặc b = 5.
b. Để số 5a43b chia hết cho 2, 3 và 5, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 2, nên b phải là số chẵn. Vì số chia hết cho 3, nên tổng các chữ số trong số đó phải chia hết cho 3. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 5 + a + 4 + 3 + 0 = 12 + a. Để 12 + a chia hết cho 3, ta có a = 0 hoặc a = 3 hoặc a = 6 hoặc a = 9.
- Nếu b = 5, thì tổng các chữ số là 5 + a + 4 + 3 + 5 = 17 + a. Để 17 + a chia hết cho 3, ta có a = 1 hoặc a = 4 hoặc a = 7.
Vậy, các giá trị thỏa mãn là a = 0 hoặc a = 3 hoặc a = 6 hoặc a = 9, và b = 0 hoặc b = 5.
c. Để số 735a2b chia hết cho 5 và 9, nhưng không chia hết cho 2, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Vì số chia hết cho 9, nên tổng các chữ số trong số đó phải chia hết cho 9. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 7 + 3 + 5 + a + 2 + 0 = 17 + a. Để 17 + a chia hết cho 9, ta có a = 7 hoặc a = 8.
- Nếu b = 5, thì tổng các chữ số là 7 + 3 + 5 + a + 2 + 5 = 22 + a. Để 22 + a chia hết cho 9, ta có a = 2 hoặc a = 5 hoặc a = 8.
Vậy, các giá trị thỏa mãn là a = 2 hoặc a = 5 hoặc a = 7 hoặc a = 8, và b = 0 hoặc b = 5.
Bài 5: Để xác định xem tổng A có chia hết cho 8 hay không, ta cần tính tổng A và kiểm tra xem nó có chia hết cho 8 hay không.
NA
2
6 tháng 6 2017
Để 3x05y \(⋮5\)=) y = 0 hoặc 5
* Với y = 0 =) 3x05y = 3x050
Để 3x050\(⋮3\)=) (3+x+0+5+0)\(⋮3\)
=) 8+x\(⋮3\)
Vì Để 8+x không chia hết 9 mà lại chia hết 3
=) x = { 4,7 }
* Với y = 5 =) ...
6 tháng 6 2017
Đặt 3x05y = A với x, y < 10
=> \(y\in\left\{0;5\right\}\)
* nếu A = 3x050
=> để A \(⋮\)3 thì \(x\in\left\{1;4;7\right\}\)
Mà A k chia hết cho 9 => \(x\in\left\{4;7\right\}\)
* nếu A = 3x055
=> để A \(⋮\)3 thì \(x\in\left\{2;5;8\right\}\)
Mà A k chia hết cho 9 => \(x\in\left\{2;8\right\}\)
Vậy: ..................
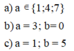
Ta có 745a ⋮ 3 ⇒ ( 7 + 4 + 5 + a ) ⋮ 3
⇒ ( 16 + a ) ⋮ 3
Vì 0 ≤ a ≤ 9 nên 16 ≤ 16 + a ≤ 25 mà 16 + a chia hết cho 3 ; không chia hết cho 9 nên ( 16 + a ) ϵ { 18 ; 21 ; 24 }
Nếu 16 + a = 18 ⇒ a = 2
16 + a = 21 ⇒ a = 5
16 + a = 24 ⇒ a = 8
Vậy a ϵ { 2 ; 5 ; 8 }
thanks