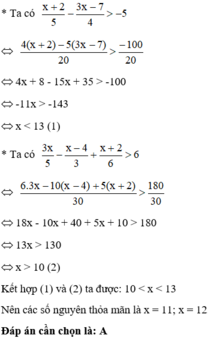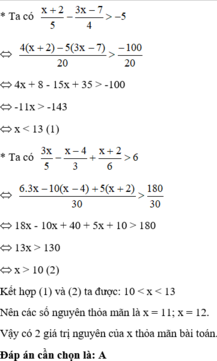Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 5. Tìm các số x thỏa mãn cả hai bất phương trình sau x>3 và x<8
A. x<8
b. 3<x<8
c. 3>x>8
d. x>3
câu 6: tìm các số x thỏa mãn cả 2 bất phương trình sau x>5 và x>3
A. x<5
B. 3<x<5
C. x>3
D. c>5


b, \(\frac{3x-2}{5}\ge\frac{x+1,6}{2}\)
=> \(6x-4\ge5x+8\)
=> \(x-12\ge0\)
=> \(x\ge12\)
bpt 2: \(\frac{6-2x+5}{6}>\frac{3-x}{4}\)
=> \(\frac{11-2x}{6}>\frac{3-x}{4}\)
=> \(44-8x>18-6x\)
=> \(x< 13\)
Vậy để t/m cả 2 bpt thì : \(12\le x< 13\)

Ta có: 4,2 – (3 – 0,4x) > 0,1x + 0,5
⇔ 4,2 – 3 + 0,4x > 0,1x + 0,5
⇔ 0,4x – 0,1x > 0,5 – 1,2
⇔ 0,3x > - 0,7
⇔ x > - 7/3
Vậy số nguyên bé nhất cần tìm là -2.

a, \(\frac{2x}{5}+\frac{3-2x}{3}\ge\frac{3x+2}{2}\)
\(\Leftrightarrow\frac{12x}{30}+\frac{30-20x}{30}\ge\frac{45x+30}{30}\)
\(\Leftrightarrow12x+30-20x\ge45x+30\)
\(\Leftrightarrow-8x+30\ge45x+30\Leftrightarrow-8x-45x\ge0\)
\(\Leftrightarrow-53x\ge0\Leftrightarrow x\le0\)
Vậy tập nghiệm của BFT là S = { x | x =< 0 }

\(\left(x+1\right)\left(x-1\right)< 0\)
\(\Leftrightarrow x^2-1< 0\)
\(\Leftrightarrow x^2< 1\)
\(\Leftrightarrow\hept{\begin{cases}x< 1\\x>-1\end{cases}}\)
Vậy giá trị thỏa mãn của x là 0