Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b, \(3x=2y\Rightarrow\frac{x}{2}=\frac{y}{3}\)
\(7y=5z\Rightarrow\frac{y}{5}=\frac{z}{7}\)
\(\frac{x}{2}=\frac{y}{3};\frac{y}{5}=\frac{z}{7}\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{21}\)
áp dụng dãy tỉ số bằng nhau :
\(\frac{x-y+z}{10-15+21}=\frac{32}{16}=2\)
x = 2 . 10 = 20
y = 2 . 15 = 30
z = 2 . 21 = 42
Vậy : .....
a, \(\frac{x}{3}=\frac{y}{4};\frac{y}{5}=\frac{z}{7}\)
MSC của y là : 20
Có: \(\frac{x}{15}=\frac{y}{20}=\frac{z}{28}\)
Áp dụng dãy tỉ số bằng nhau, ta có:
\(2x+3y-z=186\)
\(\Rightarrow2.15+3.20-28=30+60-28=62\)
\(\frac{186}{62}=3\)
x = 3 . 15 = 45
y = 3 . 20 = 60
z = 3 . 28 = 84
Vậy: .....

b. \(\frac{x^3}{8}=\frac{y^3}{64}=\frac{z^3}{216}\Rightarrow\left(\frac{x}{2}\right)^3=\left(\frac{y}{4}\right)^3=\left(\frac{z}{6}\right)^3\Rightarrow\frac{x}{2}=\frac{y}{4}=\frac{z}{6}\)
\(\Rightarrow\frac{x^2}{4}=\frac{y^2}{16}=\frac{z^2}{36}\)
Theo t/c dảy tỉ số = nhau:
\(\frac{x^2}{4}=\frac{y^2}{16}=\frac{z^2}{36}=\frac{x^2+y^2+z^2}{4+16+36}=\frac{14}{56}=\frac{1}{4}\)
=> \(\frac{x^2}{4}=\frac{1}{4}\Rightarrow x^2=\frac{1}{4}.4=1=1^2=\left(-1\right)^2\Rightarrow x=\)+1
=> \(\frac{y^2}{16}=\frac{1}{4}\Rightarrow y^2=\frac{1}{4}.16=4=2^2=\left(-2\right)^2\Rightarrow y=\)+2
=> \(\frac{z^2}{36}=\frac{1}{4}\Rightarrow z^2=\frac{1}{4}.36=9=3^2=\left(-3\right)^2\Rightarrow z=\)+3
Vậy có 2 cặp (x;y;z) là: (1;2;3) và (-1;-2;-3).
a. Áp dụng t/c tỉ số = nhau làm tương tự.

a ) \(7x=3y\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{7}\) và \(x-y=16\)
Theo tính chất của dãy tỉ số bằng nhau, ta có :
\(\dfrac{x}{3}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=\dfrac{16}{-4}=-4\)
\(\Rightarrow\dfrac{x}{3}=-4\Leftrightarrow x=-12\)
\(\Rightarrow\dfrac{x}{7}=-4\Leftrightarrow x=-28\)
Vậy .................
b ) \(\dfrac{x}{2}=\dfrac{y}{5}\)
Đặt \(\dfrac{x}{2}=\dfrac{y}{5}=k\)
\(\Leftrightarrow x=2k;y=5k\)
Mà \(x.y=10\)
\(\Rightarrow2k.5k=10\Leftrightarrow10k^2=10\Leftrightarrow\left[{}\begin{matrix}k=1\\k=-1\end{matrix}\right.\)
2 TH xảy ra :
-Với k = 1 , thì :
\(\left[{}\begin{matrix}x=2.1=2\\y=5.1=5\end{matrix}\right.\)
- Với k=-1, thì :
\(\left[{}\begin{matrix}x=-2\\y=-5\end{matrix}\right.\)
Vậy.............
c ) \(\dfrac{x}{4}=\dfrac{y}{3}\Leftrightarrow\dfrac{2x}{8}=\dfrac{5y}{15}\) và \(2x+5y=69\)
Theo tính chất của dãy tỉ số bằng nhau, ta có :
\(\dfrac{2x}{8}=\dfrac{5y}{15}=\dfrac{2x+5y}{8+15}=\dfrac{69}{23}=3\)
\(\Rightarrow\dfrac{2x}{8}=3\Leftrightarrow2x=24\Leftrightarrow x=12\)
\(\Rightarrow\dfrac{5y}{15}=3\Leftrightarrow5y=45\Leftrightarrow y=9\)
d ) \(5x=3y\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{5}\Leftrightarrow\dfrac{4x}{12}=\dfrac{3y}{15}\) và \(4x-3y=-99\)
Theo tính chất của dãy tỉ số bằng nhau , ta có :
\(\dfrac{4x}{12}=\dfrac{3y}{15}=\dfrac{4x-3y}{12-15}=\dfrac{-99}{-3}=33\)
\(\Leftrightarrow\dfrac{4x}{12}=33\Leftrightarrow4x=396\Leftrightarrow x=99\)
\(\Rightarrow\dfrac{3y}{15}=33\Leftrightarrow3y=495\Leftrightarrow y=165\)
Vậy .......
a. \(7x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{7}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{3}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=\dfrac{16}{-4}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=3.\left(-4\right)=-12\\y=7.\left(-4\right)=-28\end{matrix}\right.\)

Từ \(\dfrac{x}{3}=\dfrac{y}{5}\)=> \(\dfrac{x^2}{9}=\dfrac{y^2}{25}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\dfrac{x^2}{9}=\dfrac{y^2}{25}=\dfrac{x^2-y^2}{9-25}=\dfrac{-4}{-16}=\dfrac{1}{4}\)
=> \(\left\{{}\begin{matrix}\dfrac{x^2}{9}=\dfrac{1}{4}\\\dfrac{y^2}{25}=\dfrac{1}{4}\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x^2=\dfrac{9}{4}\\y^2=\dfrac{25}{4}\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}\left\{{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}y=\dfrac{5}{2}\\y=-\dfrac{5}{2}\end{matrix}\right.\end{matrix}\right.\)

Ta có :
\(A=\left(-\frac{2}{5}x^2y\right)\left(\frac{15}{8}xy^2\right)\left(-x^3y^2\right)\)
\(\Rightarrow A=\left(-\frac{2}{5}.\frac{15}{8}\right)\left(x^2.x.-x^3\right)\left(y.y^2.y^2\right)\)
\(\Rightarrow A=-\frac{3}{4}.-x^6.y^5\)
\(\Rightarrow A=-\frac{3}{4}.\left(-1\right)x^6y^5\)
\(\Rightarrow A=\frac{3}{4}x^6y^5\)
Lại có :
\(\frac{x}{3}=\frac{y}{2}\)và \(x+3y=3\)
ADTCDTSBN , ta có :
\(\frac{x}{3}=\frac{y}{2}=\frac{3y}{6}=\frac{x+3y}{3+6}=\frac{3}{9}=\frac{1}{3}\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{3}=\frac{1}{3}\\\frac{y}{2}=\frac{1}{3}\end{cases}\Rightarrow\hept{\begin{cases}x=\frac{1}{3}.3=1\\y=\frac{1}{3}.2=\frac{2}{3}\end{cases}}}\)
Thay \(x=1;y=\frac{2}{3}\)vào A ta được :
\(A=\frac{3}{4}.1^6.\left(\frac{2}{3}\right)^5\)
\(\Rightarrow A=\frac{3}{4}.\frac{32}{243}\)
\(\Rightarrow A=\frac{8}{81}\)
Vậy ...
ta có hai cách giải
cách 1:
gọi x/3=y/2=k
=> x=3k và y=2k
vì x+3y=3 => 3k+6k=3
=> 9k=3 => k=1/3
suy ra x=1 và y= 2/3
* Thay vào x;y vào phép tính trên rồi tự tính nhé
nếu k cho mik mik sẽ gợi ý cách còn lại
THANKS

Đang rảnh nên lm linh tinh thử và kết quả là
Đặt \(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=k\)
\(\Leftrightarrow\hept{\begin{cases}x-1=2k\\y-2=3k\\z-3=4k\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2k+1\\y=3k+2\\z=4k+3\end{cases}}\)
Thay x = 3k + 1 ; y = 3k + 2 và z = 3k + 3 vào 2x + 3y - z = 50 ta có
2. ( 3k + 1 ) + 3 . ( 3k + 2 ) - ( 4k + 3 ) = 50
<=> 6k + 2 + 9k + 6 - 4k - 3 = 50
<=> ( 6k + 9k - 4k ) + ( 2 + 6 - 3 ) = 50
<=> 11k + 5 = 50
<=> 11k = 45
<=> \(k=\frac{45}{11}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{45}{11}.2+1\\y=\frac{45}{11}.3+2\\z=\frac{45}{11}.4+3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{90}{11}+1=\frac{101}{11}\\y=\frac{135}{11}+2=\frac{157}{11}\\z=\frac{180}{11}+3=\frac{213}{11}\end{cases}}\)
Vậy ....
K thì thôi nhá
@@ Học tốt

\(x:y:z=3:4:5\)
\(\Rightarrow\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
Đặt \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=k\)
\(\Rightarrow x=3k;y=4k;z=5k\)
Khi đó:\(5z^2-3x^2-2y^2=594\) trở thành:
\(5\cdot25k^2-3\cdot9k^2-2\cdot16k^2=594\)
\(125k^2-27k^2-32k^2=594\)
\(66k^2=594\)
\(k^2=9\)
\(k=\pm3\)
Bạn thay vào rồi tính

Hướng dẫn(hướng làm:v) :
Từ \(3\left(x-1\right)=2\left(y-2\right)\)
\(\Rightarrow\frac{x-1}{2}=\frac{y-2}{3}\)(1) (chia hai vế của đẳng thức trên cho 6)
Từ: \(4\left(y-2\right)=3\left(z-3\right)\)
\(\Rightarrow\frac{y-2}{3}=\frac{z-3}{4}\) (2) (chia cả hai vế của đẳng thức cho 12)
Từ (1) và (2) \(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\)
Đặt \(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=k\)
\(\Rightarrow x=2k+1;y=3k+2;z=4k+3\)
Giờ thay x, y, z bởi cái bên trên vào giả thiết 2x + 3y - z = 50 để tìm k.
Tử đó thay ngược lại ta sẽ tìm được x, y, z.
P/s: Bên trên là hướng làm, khi tính toán có thể sai sót, bạn tự check lại. Mình bận nên ko thể làm full được.
Xin lỗi các bn nhé đây mới là đề bài đúng vừa nãy mk viết sai mong các bn thông cảm![]()

Ta có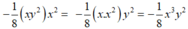 không đồng dạng với
32
x
2
y
3
không đồng dạng với
32
x
2
y
3
Chọn đáp án B