Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Đường thẳng ( d 1 ): ax + 2y = -3 đi qua điểm M(3; 9) nên tọa độ điểm M nghiệm đúng phương trình đường thẳng.
Ta có: a.3 + 2.9 = -3 ⇔ 3a + 18 = -3 ⇔ 3a = -21 ⇔ a = -7
Phương trình đường thẳng ( d 1 ): -7x + 2y = -3
*Đường thẳng ( d 2 ): 3x – by = 5 đi qua điểm N(-1; 2) nên tọa độ điểm N nghiệm đúng phương trình đường thẳng.
Ta có: 3.(-1) – b.2 = 5 ⇔ -3 – 2b = 5 ⇔ 2b = -8 ⇔ b = -4
Phương trình đường thẳng ( d 2 ): 3x + 4y = 5
*Tọa độ giao điểm của (
d
1
) và (
d
2
) là nghiệm của hệ phương trình: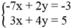
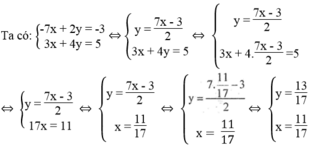

a/ bạn tự làm
b/ \(\Rightarrow y=0\Rightarrow\dfrac{1}{2}x+2=0\) giải PT tìm hoành độ x
c/ \(\Rightarrow x=0\Rightarrow y=0+2=2\)
d/ \(\Rightarrow\dfrac{1}{2}x+2=-x+2\) Giải PT tìm hoành độ x của C rồi thay vào d1 hoặc d2 để tìm tung độ y của C

*Đường thẳng ( d 1 ): 5x – 2y = c đi qua điểm A(5; -1) nên tọa độ điểm A nghiệm đúng phương trình đường thẳng.
Ta có: 5.5 – 2.(-1) = c ⇔ 25 + 2 = c ⇔ c = 27
Phương trình đường thẳng ( d 1 ): 5x – 2y = 27
*Đường thẳng ( d 2 ): x + by = 2 đi qua điểm B(-7; 3) nên tọa độ điểm B nghiệm đúng phương trình đường thẳng.
Ta có: -7 + 3b = 2 ⇔ 3b = 9 ⇔ b = 3
Phương trình đường thẳng ( d 2 ): x + 3y = 2
*Tọa độ giao điểm của (
d
1
) và (
d
2
) là nghiệm của hệ phương trình:![]()
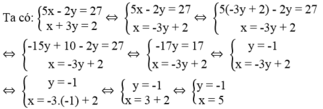
Vậy tọa độ giao điểm của ( d 1 ) và ( d 2 ) là (5; -1).

Do (d1) song song với đường thẳng y = 2x nên a = 2
(d1): y = 2x + b
Thay tọa độ điểm (1; -1) vào (d) ta được:
2.1 + b = -1
⇔ b = -1 - 2
⇔ b = -3
Vậy (d1): y = 2x - 3
b) x = 0 ⇒ y = -3
*) Đồ thị:
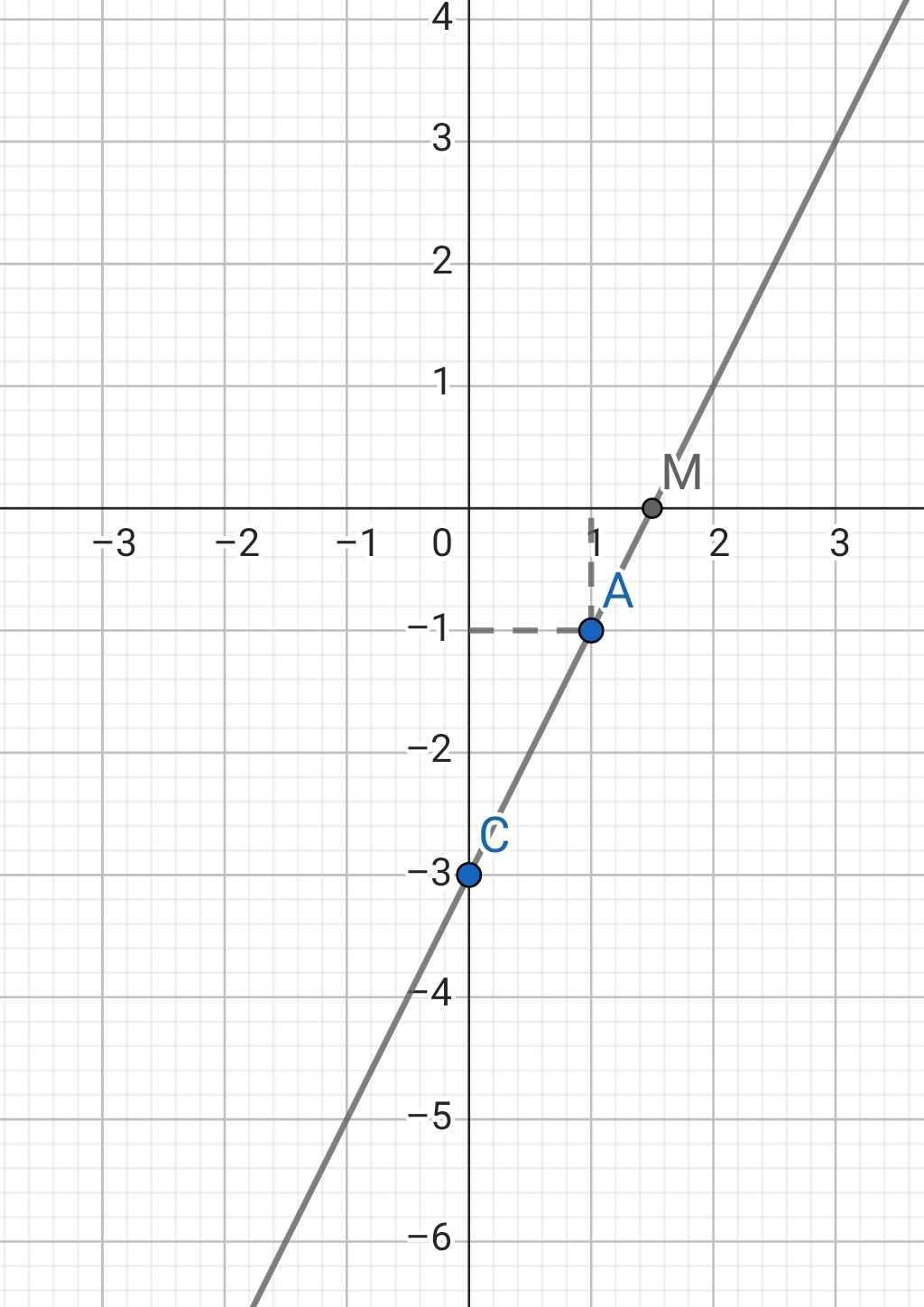
c) Phương trình hoành độ giao điểm của (d1) và (d2):
2x - 3 = 1/2 x + 1
⇔ 2x - 1/2 x = 1 + 3
⇔ 3/2 x = 4
⇔ x = 4 : 2/3
⇔ x = 8/3
⇒ y = 2.8/3 - 3 = 7/3
Vậy tọa độ giao điểm của (d1) và (d2) là (8/3; 7/3)
d) Ta có:
Gọi a là góc cần tính
⇒ tan(a) = 2
⇒ a ≈ 63⁰
(b) và (d) bạn tự xem kiến thức vẽ rồi áp dụng công thức tan là làm được nha=)
a)
Đồ thị hàm số (d1)// đường thẳng `y=2x`
=> \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b\ne0\end{matrix}\right.\)
=> `y=2x+b`
Do hàm số `y=2x+b` đi qua điểm `(1;-1)` nên `x=1`, `y=-1`:
`-1=2.1+b`
=> `b=-3`
Vậy hàm số `y=ax+b` là `y=2x-3`
c)
Ta có PTHĐGĐ giữa `d_1` và `d_2`:
\(2x-3=\dfrac{1}{2}x+1\\ \Rightarrow x=\dfrac{8}{3}\Rightarrow y=\dfrac{7}{3}\)
Vậy `E=`\(\left(\dfrac{8}{3};\dfrac{7}{3}\right)\)
$HaNa$

1, PT hoành độ giao điểm: \(2x+4=-x+1\Leftrightarrow x=-1\Leftrightarrow y=0\)
\(\Leftrightarrow A\left(-1;0\right)\)
Vậy \(A\left(-1;0\right)\) là tọa độ giao điểm 2 đths
2, Đt cần tìm //(d1)\(\Leftrightarrow a=2;b\ne4\)
Đt cần tìm đi qua M(-1;3) nên \(-a+b=3\Leftrightarrow-2+b=3\Leftrightarrow b=5\left(tm\right)\)
Vậy đths là \(y=2x+5\)
3, PT giao điểm d1 với trục hoành là \(y=0\Leftrightarrow2x+4=0\Leftrightarrow x=-2\Leftrightarrow B\left(-2;0\right)\)
PT giao điểm d2 với trục hoành là \(y=0\Leftrightarrow-x+1=0\Leftrightarrow x=1\Leftrightarrow C\left(1;0\right)\)
Do đó \(BC=\left|-2\right|+\left|1\right|=3;OA=\left|-1\right|=1\)
Vậy \(S_{ABC}=\dfrac{1}{2}OA\cdot BC=\dfrac{3}{2}\left(đvdt\right)\)
Bài I (3,0 điểm) Cho hai biểu thức A= x−9 và B= 3 + 2 +x−5 x−3 với x 0,x 9.
x−3 x−3 x+3 x−9
1) Khi x=81, tính giá trị của biểu thức A.
2) Rút gọn biểu thức B.
3) Tìm x để A = 5.
4) Với x 9, tìm giá trị nhỏ nhất của biểu thức P AB= .
giải giúp nốt cho minh luon nhe

a, bạn tự vẽ nhé
b, Hoành độ giao điểm thỏa mãn phương trình
\(2x-3=-3x+7\Leftrightarrow5x=10\Leftrightarrow x=2\)
Thay vào ptđt d1 ta được : \(y=4-3=1\)
Vậy d1 cắt d2 tại A(2;1)
a: Theo đề, ta có hệ:
2a+b=-1 và a+b=-3
=>a=2 và b=-5
b; tọa độ giao là:
2x+y=-3 và 3x-2y=-1
=>x=-1 và y=-1