
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(\dfrac{P}{x+2}=\dfrac{x^2+5x+6}{x^2+4x+4}\)
\(\Leftrightarrow\dfrac{P}{x+2}=\dfrac{\left(x+2\right)\left(x+3\right)}{\left(x+2\right)^2}=\dfrac{x+3}{x+2}\)
hay P=x+3

a: a+b=5
=>(a+b)^2=25
=>a^2+b^2+2ab=25
=>2ab=12
=>ab=6
mà a+b=5
nên a,b là các nghiệm của phương trình:
x^2-5x+6=0
=>x=2 hoặc x=3
=>(a,b)=(2;3) hoặc (a,b)=(3;2)
b: a^2-b^2=34
=>(a+b)(a-b)=34
=>a+b=17
mà a-b=2
nên a=19/2 và b=19/2-2=15/2

a: A+2xy^2-x^2y-B=3x^2y-4xy^2
=>A-B=3x^2y-4xy^2-2xy^2+x^2y=4x^2y-6xy^2
=>A=4x^2y; B=6xy^2
b: 5xy^2-A-6x^2y+B=-7xy^2+8x^2y
=>-A+B=-7xy^2+8x^2y-5xy^2+6x^2y=14x^2y-12xy^2
=>A=12xy^2; B=14x^2y
c: 5xy^3-A-5/8x^3y+B=2+1/4xy^3-7/6x^3y
=>-A+B=2+1/4xy^3-7/6x^3y-5xy^3+5/8x^3y
=>B-A=-19/4xy^3-13/24x^3y+2
=>B=-19/4xy^3; A=13/24x^3y-2

`A+B=x^4 +5x^3 -x^2 -x+1+x^4 +2x^3 -2x^2 -3x+2`
`=2x^4 +7x^3 -3x^2 -4x+3`
`A-B=x^4+5x^3-x^2-x+1-(x^4 +2x^3-2x^2-3x+2)`
`=x^4+5x^3-x^2-x+1-x^4-2x^3+2x^2+3x-2`
`=3x^3+x^2+2x-1`

Bài 1:
a: Ta có: \(A=\left(k-4\right)\left(k^2+4k+16\right)-\left(k^3+128\right)\)
\(=k^3-64-k^3-128\)
=-192
b: Ta có: \(B=\left(2m+3n\right)\left(4m^2-6mn+9n^2\right)-\left(3m-2n\right)\left(9m^2+6mn+4n^2\right)\)
\(=8m^3+27n^3-27m^3+8n^3\)
\(=-19m^3+35n^3\)
Bài 4:
a: Ta có: \(\left(x-1\right)^3+\left(2-x\right)\left(4+2x+x^2\right)+3x\left(x+2\right)=16\)
\(\Leftrightarrow x^3-3x^2+3x-1+8-x^3+3x^2+6x=16\)
\(\Leftrightarrow9x=9\)
hay x=1
b: ta có: \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x^2-2\right)=15\)
\(\Leftrightarrow x^3+8-x^3+2x=15\)
\(\Leftrightarrow2x=7\)
hay \(x=\dfrac{7}{2}\)


`@` `\text {Ans}`
`\downarrow`
`a,`
`(2x - 1)^2 - 25 = 0`
`<=> (2x - 1)^2 = 25`
`<=> (2x - 1)^2 = (+-5)^2`
`<=>`\(\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Vậy, `S = {-2; 3}`
`b,`
`8x^3 - 50x = 0`
`<=> x(8x^2 - 50) = 0`
`<=>`\(\left[{}\begin{matrix}x=0\\8x^2-50=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\8x^2=50\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\x^2=\dfrac{25}{4}\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\x=\pm\dfrac{5}{2}\end{matrix}\right.\)
Vậy, `S = {-5/2; 0; 5/2}.`
a) (2x - 1)² - 25 = 0
(2x - 1)² - 5² = 0
(2x - 1 - 5)(2x - 1 + 5) = 0
(2x - 6)(2x + 4) = 0
2x - 6 = 0 hoặc 2x + 4 = 0
*) 2x - 6 = 0
2x = 6
x = 3
*) 2x + 4 = 0
2x = -4
x = -2
Vậy x = -2; x = 3
b) 8x³ - 50x = 0
2x(4x² - 25) = 0
2x[(2x)² - 5²] = 0
2x(2x - 5)(2x + 5) = 0
2x = 0 hoặc 2x - 5 = 0 hoặc 2x + 5 = 0
*) 2x = 0
x = 0
*) 2x - 5 = 0
2x = 5
x = 5/2
*) 2x + 5 = 0
2x = -5
x = -5/2
Vậy x = -5/2; x = 0; x = 5/2
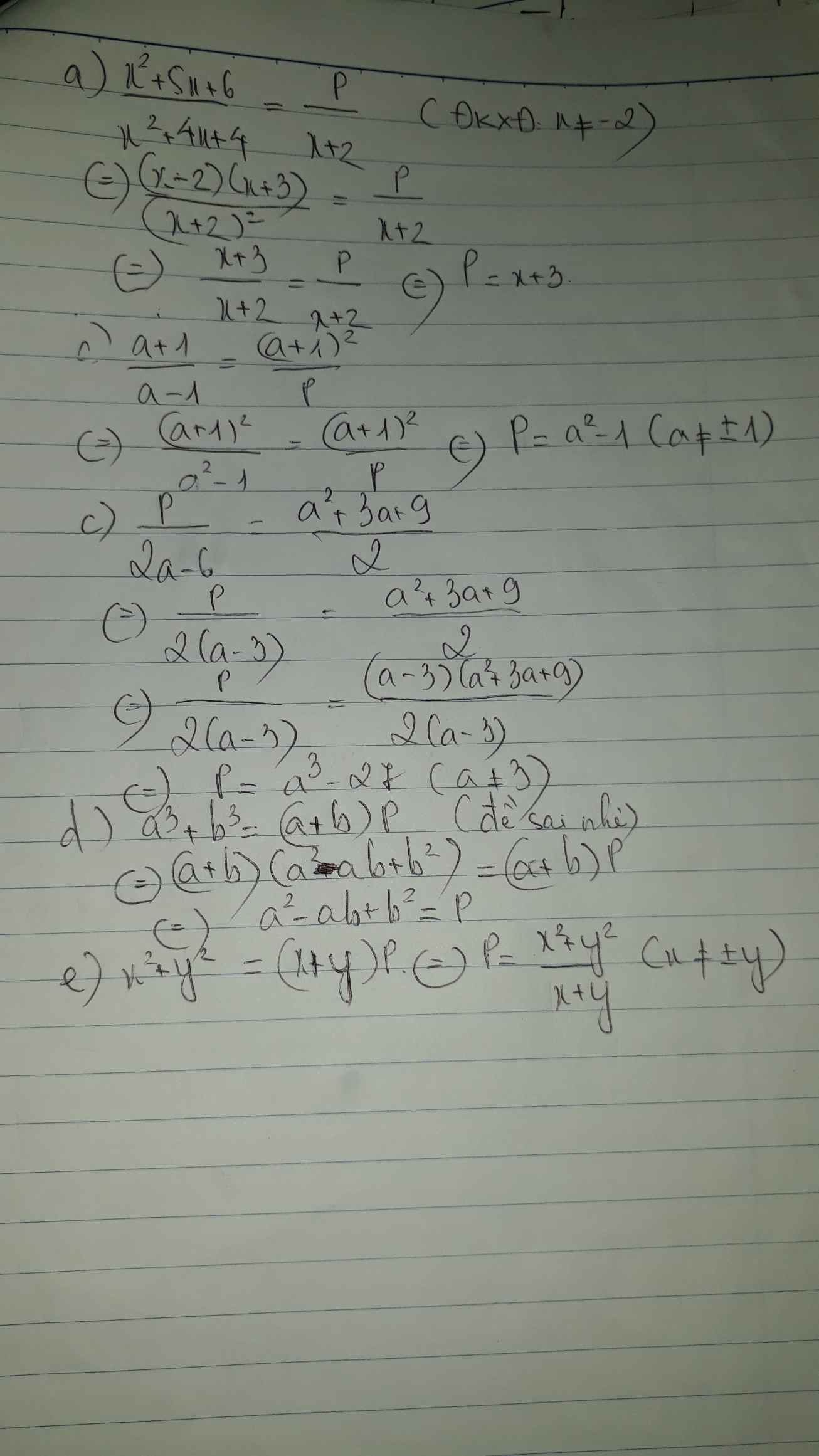
a - b = 6
=> ( a - b )2 = 36
=> a2 - 2ab + b2 = 36
<=> a2 + 2ab + b2 - 4ab = 36
<=> ( a + b )2 - 4.16 = 36
<=> ( a + b )2 = 100
<=> a + b = ±10