Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo câu 1 link:Câu hỏi của Ngọc Anh Dũng - Toán lớp 8 - Học toán với OnlineMath

a)gọi 3 số đó là x;x+1;x+2
Vì tích của 2 số sau lớn hơn tích của 2 số đầu là 180 nên ta có phương trình:
(x+1)(x+2)-x(x+1)=180
<=>x2+3x+2-x2-x=180
<=>2x+2=180
<=>2x=90
<=>x=45
vậy 2 số đó là 45;46;47
b) gọi 4 số đó là a;a+1;a+2;a+3 ( a \(\ge\)0 )
vì tích của 2 số sau lớn hơn tích của 2 số đầu là 34 nên ta có:
(a+2)(a+3)-a.(a+1)=34
<=>a2+5a+6-a2-a=34
<=>4a+6=34
<=>4a=28
<=>a=7
Vậy 4 số đó là: 7;8;9;10

gọi 3 số chẵn liên tiếp là a; a+2;a+4
Ta có: (a+2)(a+4)-a(a+2)=192
\(a^2\)+4a+2a+8-\(a^2\)-2a=192
4a+8 =192
4a = 192 - 8= 184
a = 184:4=46
Vậy 3 số đó là 46;48;50

Gọi ba số tự nhiên liên tiếp là x;x+1;x+2
Theo đề, ta có phương trình:
\(\left(x+1\right)\left(x+2\right)-x\left(x+1\right)=29\)
\(\Leftrightarrow x^2+3x+2-x^2-x=29\)
\(\Leftrightarrow2x+2=29\)
Đề sai rồi bạn

Gọi 3 số cần tìm là: a-1 ; a ; a+1
Theo bài ra , ta có:
\(a\left(a+1\right)-a\left(a-1\right)=100\)
\(\Rightarrow a^2+a-a^2+a=100\)
\(\Rightarrow2a=100\)
\(\Rightarrow a=50\)
Vậy.
Gọi 3 số tự nhiên liên tiếp có dạng là : \(a;a+1;a+2\left(a\inℕ\right)\)
Vì tích của 2 số sau lớn hơn tích của 2 số đầu là 100 nên ta có :
\(\left(a+1\right)\left(a+2\right)-a\left(a+1\right)=100\)
\(\Leftrightarrow a^2+2a+a+2-a^2-a=100\)
\(\Leftrightarrow\left(a^2-a^2\right)+\left(2a+a-a\right)=100-2\)
\(\Leftrightarrow2a=98\)
\(\Leftrightarrow a=49\)
\(\Rightarrow\hept{\begin{cases}a+1=49+1=50\\a+2=49+2=51\end{cases}}\)
Vậy 3 số tự nhiên liên tiếp cần tìm là : \(49;50;51\)
- Chúc bạn học tốt -
_Minh ngụy_

gọi 3 số chẵn liên tiếp là a; a+2;a+4
Ta có: (a+2)(a+4)-a(a+2)=192
a2a2+4a+2a+8-a2a2-2a=192
4a+8 =192
4a = 192 - 8= 184
a = 184:4=46
Vậy 3 số đó là 46;48;50
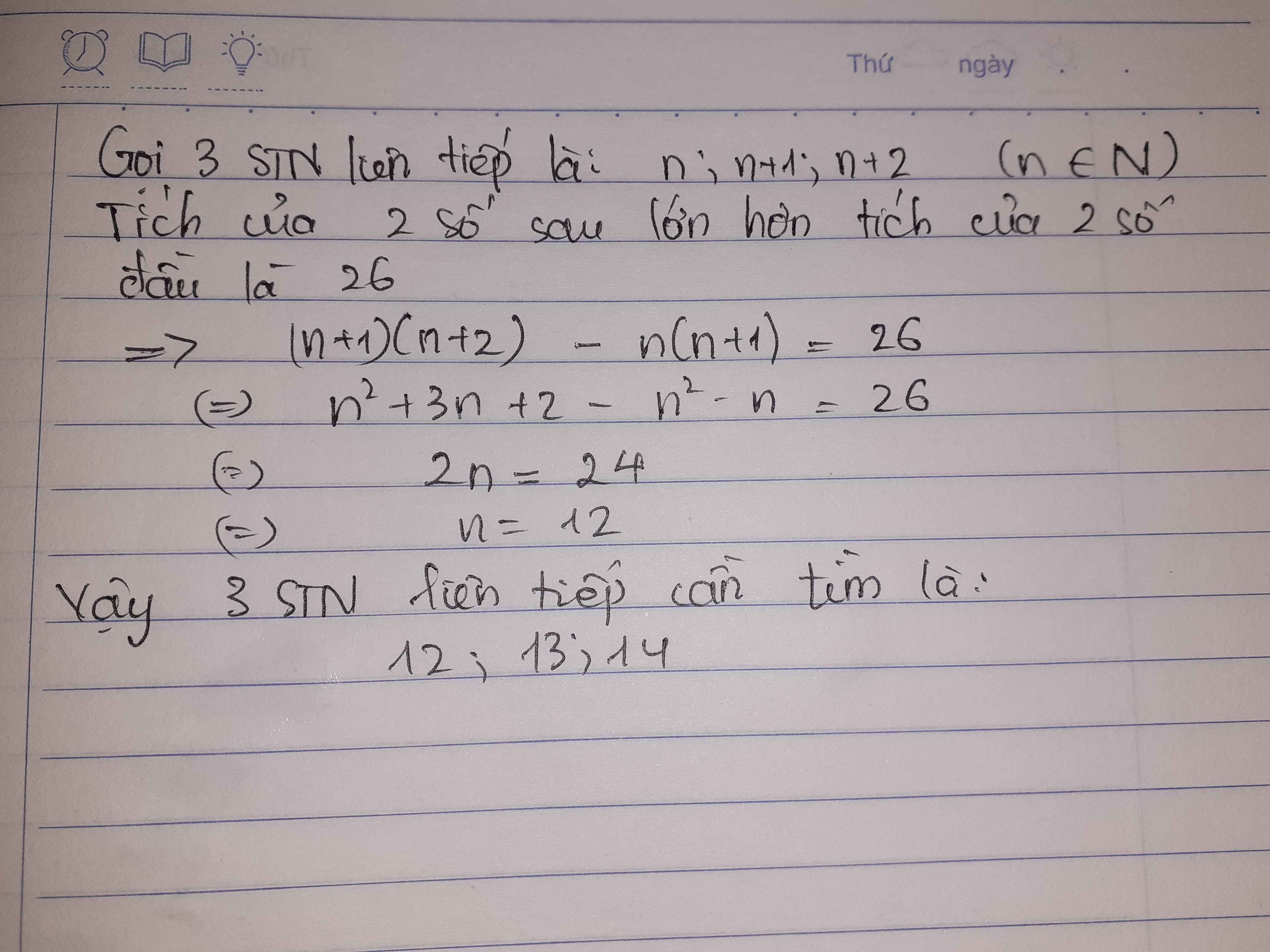
Gọi ba số cần tìm là n ; n + 1 ; n + 2 ( n ∈ N )
Theo đề bài ta có : ( n + 1 )( n + 2 ) - n( n + 1 ) = 4040
⇔ n2 + 3n + 2 - n2 - n = 4040
⇔ 2n + 2 = 4040
⇔ 2n = 4038
⇔ n = 2019 ( tm )
=> n = 2019 ; n + 1 = 2020 ; n + 2 = 2021
Vậy ba số cần tìm là 2019 ; 2020 ; 2021