Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Ta có y’=-2x; y’(1)=-2. Phương trình tiếp tuyến của y = 4 - x 2 tại điểm (1,3) là
(d):y= -2(x-1)+3=-2x+5.
Đường thẳng (d) cắt trục hoành tại điểm A(5/2; 0) và cắt trục tung tại B(0;5).
Ta có: OA = 5/2; OB = 5
Diện tích tam giác OAB vuông tại O là 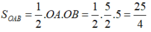

Hàm số xác định với mọi \(x\ne1\). Ta có : \(y'=\frac{-4}{\left(x-1\right)^2}\)
Gọi \(M\left(x_0;y_0\right);\left(x_0\ne1\right)\) là tiếp điểm, suy ra phương trình tiếp tuyến của (C) :
\(\Delta:y=\frac{-4}{\left(x_0-1\right)^2}\left(x-x_0\right)+\frac{2x_0+2}{x_0-1}\)
a) Vì tiếp tuyến có hệ số góc bằng -4 nên ta có :
\(\frac{4}{\left(x_0-1\right)^2}=-16\Leftrightarrow\left[\begin{array}{nghiempt}x_0=\frac{3}{2}\\x_0=\frac{1}{2}\end{array}\right.\)
* \(x_0=\frac{3}{2}\Rightarrow y_0=10\Rightarrow\Delta=-16\left(x-\frac{3}{2}\right)+10\) hay \(y=-16x+22\)
* \(x_0=\frac{1}{2}\Rightarrow y_0=-6\Rightarrow\Delta=-16\left(x-\frac{1}{2}\right)-6\) hay \(y=-16x+2\)

(C): \(y=x^3-3x^2+1\)
=>\(y'=3x^2-3\cdot2x=3x^2-6x\)
Tiếp tuyến của (C) tại điểm có x=3 có dạng là:
\(y-y\left(3\right)=f'\left(3\right)\cdot\left(x-3\right)\)
=>\(y-\left(3^3-3\cdot3^2+1\right)=\left(3\cdot3^2-6\cdot3\right)\left(x-3\right)\)
=>\(y-1=9\left(x-3\right)=9x-27\)
=>y=9x-27+1=9x-26
Gọi A(x,y) và B(x,y) lần lượt là tọa độ giao điểm của đường thẳng y=9x-26 với trục Ox và trục Oy
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\9x-26=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{26}{9}\\y=0\end{matrix}\right.\)
Tọa độ B là; \(\left\{{}\begin{matrix}x=0\\y=9\cdot0-26=-26\end{matrix}\right.\)
Vậy: A(26/9;0); B(0;-26)
\(OA=\sqrt{\left(\dfrac{26}{9}-0\right)^2+\left(0-0\right)^2}=\dfrac{26}{9}\)
\(OB=\sqrt{\left(0-0\right)^2+\left(-26-0\right)^2}=26\)
Vì Ox\(\perp\)Oy nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot26\cdot\dfrac{26}{9}=\dfrac{338}{9}\)
=>Chọn D

Ta có : \(A\left(0;\frac{1}{3}\right)\) và \(y'=4x^2-2\left(2m+1\right)x+m+2\)
Suy ra \(y'\left(0\right)=m+2\)
Tiếp tuyến của d cắt Ox tại \(B\left(-\frac{1}{3m+6};0\right)\) (m=-2 không thỏa mãn yêu cầu bài toán)
Khi đó diện tích của tam giác tạo bởi d với 2 trục tọa độ là :
\(S=\frac{1}{2}OA.OB=\frac{1}{2}.\frac{1}{3}.\left|\frac{-1}{3m+6}\right|=\frac{1}{18\left|m+2\right|}\)
Theo giả thiết ta có : \(\frac{1}{18\left|m+2\right|}=\frac{1}{3}\Leftrightarrow\left|m+2\right|=\frac{1}{6}\)
\(\Leftrightarrow m=-\frac{13}{6}\) hoặc \(m=-\frac{11}{6}\)

Ta có : \(y'=\frac{-m-3}{\left(x-1\right)^2}\)
a) Vì \(x_0=0\Rightarrow y_0=-m-1;y'\left(x_0\right)=-m-3\)
Phương trình tiếp tuyến d của \(\left(C_m\right)\) tại điểm có hoành độ \(x_0=0\) là :
\(y=\left(-m-3\right)x-m-1\)
Tiếp tuyến đi qua \(A\) khi và chỉ khi \(3=\left(-m-3\right)4-m-1\Leftrightarrow m=-\frac{16}{5}\)
b) Ta có : \(x_0=2\Rightarrow y_0=m+5;y'\left(x_0\right)=-m-3\)
Phương trình tiếp tuyến \(\Delta\) của \(\left(C_m\right)\) tại điểm có hoành độ \(x_0=2\) là :
\(y=\left(-m-3\right)\left(x-2\right)+m+5=\left(-m-3\right)x+3m+11\)
* \(\Delta\cap Ox=A\Rightarrow A\left(\frac{3m+11}{m+3};0\right)\) với \(m+3\ne0\)
* \(\Delta\cap Oy=B\Rightarrow B\left(0;3m+11\right)\)
Suy ra diện tích tam giác OAB là : \(S=\frac{1}{2}OA.OB=\frac{1}{2}\frac{\left(3m+11\right)^2}{\left|m+3\right|}\)
Theo giả thiết bài toán suy ra \(\frac{1}{2}\frac{\left(3m+11\right)^2}{\left|m+3\right|}=\frac{25}{2}\)
\(\Leftrightarrow\left(3m+11\right)^2=25\left|m+3\right|\Leftrightarrow\)\(\left[\begin{array}{nghiempt}9m^2+66m+121=25m+75\\9m^2+66m+121=-25m-75\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}9m^2+41m+46=0\\9m^2+91m+196=0\end{array}\right.\Leftrightarrow\left[\begin{array}{nghiempt}m=-2;m=-\frac{23}{9}\\m=-7;m=-\frac{28}{9}\end{array}\right.\)

Gọi \(A\left(a;\frac{2a}{a-1}\right);B\left(b;\frac{2b}{b-1}\right);\left(a,b\ne0;a,b\ne1;a\ne b\right)\) thuộc đồ thị (C)
Khi đó hệ số góc của các đường tiếp tuyếb rại A; B lần lượt là :
\(k_1=-\frac{2}{\left(a-1\right)^2};k_2=-\frac{2}{\left(b-1\right)^2};\)
Do các đường tiếp tuyến song song nên :
\(-\frac{2}{\left(a-1\right)^2}=-\frac{2}{\left(b-1\right)^2};\)
\(\Leftrightarrow a+b=2\)
Mặt khác, ta có : \(\overrightarrow{OA}=\left(a;\frac{2a}{a-1}\right);\overrightarrow{OB}=\left(b;\frac{2b}{b-1}\right)\)
Do OAB là tam giác vuông tại O nên \(\overrightarrow{OA}.\overrightarrow{OB}=0\Leftrightarrow ab+\frac{4ab}{\left(a-1\right)\left(b-1\right)}=0\)
Ta có hệ : \(\begin{cases}a+b=2\\ab+\frac{4ab}{\left(a-1\right)\left(b-1\right)}=0\end{cases}\)
Giải hệ ta được : \(\begin{cases}a=-1\\b=3\end{cases}\) hoặc \(\begin{cases}a=3\\b=-1\end{cases}\)
Vậy 2 điểm cần tìm có tọa độ là : (-1;1) và (3;3)

\(y'=\dfrac{-3}{\left(x-2\right)^2}\)
d. Phương trình hoành độ giao điểm
\(\dfrac{x+1}{x-2}=x-\dfrac{1}{2}\Leftrightarrow2x^2-7x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{7}{2}\end{matrix}\right.\)
Tại \(x=0\Rightarrow\left\{{}\begin{matrix}y'=-\dfrac{3}{4}\\y=-\dfrac{1}{2}\end{matrix}\right.\)
Pttt: \(y=-\dfrac{3}{4}x-\dfrac{1}{2}\)
Tại \(x=\dfrac{7}{2}\Rightarrow\left\{{}\begin{matrix}y'=-\dfrac{4}{3}\\y=3\end{matrix}\right.\) tiếp tuyến: \(y=-\dfrac{4}{3}\left(x-\dfrac{7}{2}\right)+3\)
e.
Tam giác ABC là tam giác nào nhỉ? Có lẽ đó là tam giác OAB?
g.
Giao điểm (C) với Ox có tọa độ \(\left(-1;0\right)\)
\(\Rightarrow y'\left(-1\right)=-\dfrac{1}{3}\)
Phương trình tiếp tuyến:
\(y=-\dfrac{1}{3}\left(x+1\right)\)
h.
Giao điểm (C) với Oy có tọa độ \(\left(0;-\dfrac{1}{2}\right)\)
Chính là trường hợp đầu của câu d, phương trình: \(y=-\dfrac{3}{4}x-\dfrac{1}{2}\)

Lời giải:
Ta có: \(y'=-2x\) nên phương trình tiếp tuyến tại điểm \((1;3)\) là:
\(y=-2(x-1)+3\Leftrightarrow y=-2x+5\) \((d)\)
Khi đó, \(\left\{\begin{matrix} (d)\cap Ox=\left(\frac{5}{2},0\right)\\ (d)\cap Oy=(0,5)\end{matrix}\right.\)
Suy ra độ dài hai cạnh góc vuông là: \(\frac{5}{2}\) và $5$
Do đó, diện tích tam giác vuông là:
\(S=\frac{1}{2}.\frac{5}{2}.5=\frac{25}{4}\) (đơn vị diện tích)