K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 3 2022
a, Vì MA là tiếp tuyến (O) với A là tiếp điểm
=> ^MAO = 900
I là trung điểm BC => OI vuông BC
Xét tứ giác MAOI có
^MAO + MIO = 1800
mà 2 góc này đối
Vậy tứ giác MAOI là tứ giác nt 1 đường tròn
b, Xét tam giác MAB và tam giác MCA có
^M _ chung
^MAB = ^MCA ( cùng chắn cung AB )
Vậy tam giác MAB ~ tam giác MCA (g.g)
\(\dfrac{MA}{MC}=\dfrac{MB}{MA}\Rightarrow MA^2=MB.MC\)(1)
Xét tam giác MAO vuông tại A, đường cao AH
Ta có AM^2 = MH.MO ( tỉ lệ thức ) (2)
Xét tam giác MHK và tam giác MIO có
^M _ chung
^MHK = ^MIO = 900
Vậy tam giác MHK ~ tam giác MIO (g,g)
\(\dfrac{MH}{MI}=\dfrac{MK}{MO}\Rightarrow MH.MO=MK.MI\)(3)
Từ (1) ; (2) ; (3) suy ra \(MK.MI=MB.MC\)
CC
6
29 tháng 12 2023
1: Xét tứ giác OBPC có
\(\widehat{OBP}+\widehat{OCP}=90^0+90^0=180^0\)
=>OBPC là tứ giác nội tiếp
=>O,B,P,C cùng thuộc một đường tròn
2: Xét (O) có
PC,PB là các tiếp tuyến
Do đó: PC=PB
=>P nằm trên đường trung trực của CB(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OP là đường trung trực của BC
=>OP\(\perp\)BC
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)CB
Ta có: AC\(\perp\)CB
OP\(\perp\)CP
Do đó: AC//OP
có vẽ hình lun ạ
31 tháng 12 2023
1:
Ta có: ΔABC vuông tại C
mà ΔCAB nội tiếp (O)
nên O là trung điểm của AB
Xét tứ giác OBDC có \(\widehat{OBD}+\widehat{OCD}=90^0+90^0=180^0\)
nên OBDC là tứ giác nội tiếp
=>O,B,D,C cùng thuộc một đường tròn
Xét (O) có
DC,DB là các tiếp tuyến
Do đó: DC=DB
=>D nằm trên đường trung trực của CB(1)
Ta có: OC=OB
=>O nằm trên đường trung trực của CB(2)
Từ (1) và (2) suy ra OD là đường trung trực của CB
=>OD\(\perp\)CB
Ta có: AC\(\perp\)CB
CB\(\perp\)OD
Do đó: OD//AC
2: Xét (O) có
ΔBEA nội tiếp
AB là đường kính
Do đó: ΔBAE vuông tại E
=>BE\(\perp\)EA tại E
=>BE\(\perp\)AD tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(DE\cdot DA=DB^2\left(3\right)\)
Xét ΔDOB vuông tại B có BH là đường cao
nên \(DH\cdot DO=DB^2\)(4)
Từ (3) và (4) suy ra \(DE\cdot DA=DH\cdot DO\)
AH
Akai Haruma
Giáo viên
8 tháng 6 2021
Lời giải:
Gọi bán kính đáy khúc gỗ là $r$ (cm) thì:
Thể tích khúc gỗ:
$\pi r^2h=15\pi r^2$ (cm khối)
Thể tích hình nón:
$\frac{1}{3}\pi r^2h=5\pi r^2$ (cm khối)
Thể tích phần bỏ đi:
$15\pi r^2-5\pi r^2=640r$ (cm khối)
$10\pi r^2=640r$
$10\pi r=640$
$r=\frac{64}{\pi}$ (cm)
Thể tích khối nón: $5\pi r^2=5\pi.\frac{64^2}{\pi ^2}=\frac{20480}{\pi}$ (cm khối)
AH
Akai Haruma
Giáo viên
8 tháng 6 2021
Nghe đề bài có vẻ sai sai. Nếu đề là $640\pi$ (cm khối) thì bạn cũng làm tương tự, $r=8$ (cm)
CM
23 tháng 1 2017
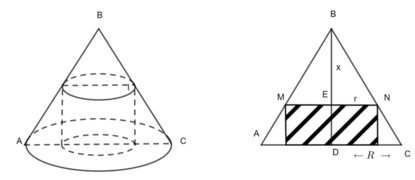
Gọi R là bán kính đáy ,h là chiều cao hình nón , r là bán kính đáy hình trụ x=BE là chiều cao phần hình nón bị cắt đi
Ta có: MN // AC
Phần bỏ đi của hình nón ít nhất tương đương với thể tích hình trụ là lớn nhất
Vì π,R,h là các hằng số nên thể tích hình trụ lớn nhất khi và chỉ khi x 2 (2h-2x) lớn nhất
Vì x + x + (2h -2x) =2h là một hằng số không đổi nên tích x.x(2h -2x) đạt giá trị lớn nhất khi
x = 2h – 2x ⇔ 3x =2h ⇒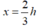 
Vậy khi phần cắt bỏ ở phía trên hình nón có chiều cao bằng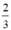 
chiều cao hình nón thì phần bỏ đi là ít nhất
1:
Ta có;ΔCAB vuông tại C
=>ΔCAB nội tiếp đường tròn đường kính AB
mà ΔCAB nội tiếp (O)
nên O là trung điểm của AB
Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=90^0+90^0=180^0\)
=>OBDC là tứ giác nội tiếp
=>O,B,D,C cùng thuộc một đường tròn
Xét (O) có
DB,DC là các tiếp tuyến
Do đó: DB=DC
=>D nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OD là đường trung trực của BC
=>OD\(\perp\)BC tại H và H là trung điểm của BC
Ta có: OD\(\perp\)BC
AC\(\perp\)BC
Do đó: OD//AC
2: Xét (O) có
ΔBEA nội tiếp
BA là đường kính
Do đó: ΔBEA vuông tại E
=>BE\(\perp\)EA tại E
=>BE\(\perp\)AD tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(DE\cdot DA=DB^2\left(3\right)\)
Xét ΔDBO vuông tại B có BH là đường cao
nên \(DH\cdot DO=DB^2\left(4\right)\)
Từ (3) và (4) suy ra \(DE\cdot DA=DH\cdot DO\)