Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Sau 6h lượng Na còn lại là:
$m=m_o.2^{-\dfrac{t}{T}}.$
Với: $2^{-\dfrac{-t}{T}}=2^{-\dfrac{6}{15}}=0,7579.$
$m=0,75.10^{-5}.24=1,8.10^{-4} g.$
Trong máu lấy ra có $m'=1,5.10^{-8} \left(mol\right)=3,6.10^{-7} \left(g\right).$
$V'=10 cm^3=10^{-2} \left(l\right).$
Vì tại cùng một thời điểm nên:
$\dfrac{V}{V'}=\dfrac{m}{m'} \Rightarrow V=V'\dfrac{m}{m'} \approx 5.$
Chọn $A$.
Đáp án B.
Trong thể tích V 0 = 10 c m 3 = 10 - 2 lít dung dịch với nồng độ 10-3 mol/lít có số mol là n = 10 - 5 mol và có khối lượng là: m 0 = n A = 24 . 10 - 5 g.
Vì N 11 24 a là chất phóng xạ nên sau 6 giờ lượng N 11 24 a còn lại là:
m = m 0 e - λ t = 24 . e ln 2 T t = 18 . 10 - 5 ( g )
Trong thể tích V 0 = 10 c m 3 máu lấy ra có 1 , 875 . 10 - 8 mol của Na, tương ứng với khối lượng chất phóng xạ: m' = n'.A = 1 , 875 . 10 - 8 .24 = 45 . 10 - 8 (g)
Vậy thể tích máu là:
V = m m ' . V 0 = 18 . 10 - 5 45 . 10 - 8 . 10 = 4 . 10 3 c m 3 = 4 ( L í t )
\(7,934.10^{-6}\)mol là lượng Na có trong máu người.
Bởi vì Na phân bố đều vào máu, nên giả sử thể tích máu của người là V thì:
\(\dfrac{V}{10}=\dfrac{7,934.10^{-6}}{1,5.10^{-8}}\)
\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.
Đáp án B.
Trong thể tích V 0 = 10 c m 3 = 10 - 2 lít dung dịch với nồng độ 10 - 3 mol/lít có số mol là n = 10 - 5 m o l và có khối lượng là: m 0 = n A = 24 . 10 - 5 g .
Vì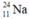 
là chất phóng xạ nên sau 6 giờ lượng 
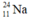còn lại là:
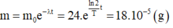
Trong thể tích
V
0
=
10
c
m
3
máu lấy ra có
1
,
875
.
10
-
8
m
o
l
của Na, tương ứng với khối lượng chất phóng xạ:
Vậy thể tích máu là:
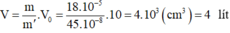
Khối lượng chất phóng xạ đã bị phân rã là
\(\Delta m = m_0(1-2^{-\frac{t}{T}}) \)
=> \(\frac{\Delta m }{m_0}= 0,75 =1- 2^{-\frac{t}{T}}\)
=> \(t = -T\ln_20,25 = 30h.\)
Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)
Đáp án A