Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Ta có: MX= 100. C5H8O2
Chú ý: Đồng phân cấu tạo nghĩa là không tính đồng phân hình học.
+ HCOOCH = CH - CH2 - CH3;
+ HCOOCH = C(CH3) - CH3;
+ CH3COOCH = CH - CH3;
+ CH3CH2COOCH = CH2

Đáp án D
MX = 3,125 . 32 = 100 —> C5H8O2
1.HCOOCH=CH-CH2-CH3 + NaOH
→ HCOONa + CH3CH2CH2CHO
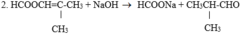
3. CH3COOCH=CH-CH3 + NaOH
→ CH3COONa + CH3CH2CHO
4. CH3CH2COOCH=CH2 + NaOH
→ CH3CH2COONa + CH3CHO

Chọn đáp án B
MX = 100 → chỉ có este X thỏa mãn là C5H8O2.
Thủy phân X cho anđehit → liên kết π nằm ở gốc ancol, este dạng …COOCH=C…
⇒ Các công thức cấu tạo thỏa mãn gồm: HCOOCH=CHCH2CH3 (1);
HCOOC=C(CH3)CH3 (2); CH3COOCH=CHCH3; C2H5COOC=CH2 (4).
⇒ Chọn đáp án B.

Đáp án B
MX = 100 → chỉ có este X thỏa mãn là C5H8O2.
Thủy phân X cho anđehit → liên kết π nằm ở gốc ancol, este dạng …COOCH=C…
=>Các công thức cấu tạo thỏa mãn gồm: HCOOCH=CHCH2CH3 (1);
HCOOC=C(CH3)CH3 (2); CH3COOCH=CHCH3; C2H5COOC=CH2 (4).

Đáp án B
MX = 100 → chỉ có este X thỏa mãn là C5H8O2.
Thủy phân X cho anđehit → liên kết π nằm ở gốc ancol, este dạng …COOCH=C…
=>Các công thức cấu tạo thỏa mãn gồm: HCOOCH=CHCH2CH3 (1); HCOOC=C(CH3)CH3 (2); CH3COOCH=CHCH3; C2H5COOC=CH2 (4).

Ta có:
Hàm \(\Psi\)được gọi là hàm chuẩn hóa nếu: \(\int\Psi.\Psi^{\circledast}d\tau=1hay\int\Psi^2d\tau=1\)
Hàm \(\Psi\)chưa chuẩn hóa là: \(\int\left|\Psi\right|^2d\tau=N\left(N\ne1\right)\)
Để có hàm chuẩn hóa, chia cả 2 vế cho N,ta có:
\(\frac{1}{N}.\int\left|\Psi\right|^2d\tau=1\Rightarrow\frac{1}{N}.\int\Psi.\Psi^{\circledast}d\tau=1\)
Trong đó: \(\Psi=\frac{1}{\sqrt{N}}.\Psi\)là hàm chuẩn hóa; \(\frac{1}{\sqrt{N}}\)là thừa số chuẩn hóa
Ta có:
\(\frac{1}{N}.\int\Psi.\Psi^{\circledast}d\tau=\frac{1}{N}.\int\left|\Psi\right|^2d\tau=1\Leftrightarrow\frac{1}{N}.\iiint\left|\Psi\right|^2dxdydz=1\)
Chuyển sang tọa độ cầu, ta có: \(\begin{cases}x=r.\cos\varphi.sin\theta\\y=r.sin\varphi.sin\theta\\z=r.\cos\theta\end{cases}\)với \(\begin{cases}0\le r\le\infty\\0\le\varphi\le2\pi\\0\le\theta\le\pi\end{cases}\)
\(\Rightarrow\frac{1}{N}.\iiint\left(r.\cos\varphi.sin\theta\right)^2.e^{-\frac{r}{a_o}}.r^2.sin\theta drd\varphi d\theta=1\)
\(\Leftrightarrow\frac{1}{N}.\int\limits^{\infty}_0r^4.e^{-\frac{r}{a_o}}dr.\int\limits^{2\pi}_0\cos^2\varphi d\varphi.\int\limits^{\pi}_0sin^3\theta d\theta=1\)
\(\Leftrightarrow\frac{1}{N}.\frac{4!}{\left(\frac{1}{a_o}\right)^5}.\int\limits^{2\pi}_0\frac{\cos\left(2\varphi\right)+1}{2}d\varphi\int\limits^{\pi}_0\frac{3.sin\theta-sin3\theta}{4}d\theta=1\)(do \(\int\limits^{\infty}_0x^n.e^{-a.x}dx=\frac{n!}{a^{n+1}}\))
\(\Leftrightarrow\frac{1}{N}.24.a^5_o.\frac{4}{3}.\pi=1\)
\(\Leftrightarrow\frac{1}{N}=\frac{1}{32.a^5_o.\pi}\)
\(\Rightarrow\)Thừa số chuẩn hóa là: \(\frac{1}{\sqrt{N}}=\sqrt{\frac{1}{32.a^5_o.\pi}}\); Hàm chuẩn hóa: \(\Psi=\frac{1}{\sqrt{N}}.\Psi=\sqrt{\frac{1}{32.a^5_o.\pi}}.x.e^{-\frac{r}{2a_o}}\)
áp dụng dk chuẩn hóa hàm sóng. \(\int\psi\psi^{\cdot}d\tau=1.\)
ta có: \(\int N.x.e^{-\frac{r}{2a_0}}.N.x.e^{-\frac{r}{2a_0}}.d\tau=1=N^2.\int_0^{\infty}r^4e^{-\frac{r}{a_0}}dr.\int_0^{\pi}\sin^3\theta d\tau.\int^{2\pi}_0\cos^2\varphi d\varphi=N^2.I_1.I_2.I_3\)
Thấy tích phân I1 có dạng tích phân hàm gamma. \(\int^{+\infty}_0x^ne^{-ax}dx=\int^{+\infty}_0\frac{\left(\left(ax\right)^{n+1-1}e^{-ax}\right)d\left(ax\right)}{a^{n+1}}=\frac{\Gamma\left(n+1\right)!}{a^{n+1}}=\frac{n!}{a^{n+1}}.\)
.áp dụng cho I1 ta được I\(I1=4!.a_0^5=24a^5_0\). tính \(I2=\int_0^{\pi}\sin^3\theta d\theta=\int_0^{\pi}\left(\cos^2-1\right)d\left(\cos\theta\right)=\frac{4}{3}\). tính tp \(I3=\int_0^{2\pi}\cos^2\varphi d\varphi=\int_0^{2\pi}\frac{\left(1-\cos\left(2\varphi\right)\right)}{2}d\varphi=\pi\)
suy ra \(\frac{N^2.24a_0^5.\pi.4}{3}=1\). vậy N=\(N=\frac{1}{\sqrt{32\pi a_0^5}}\). hàm \(\psi\) sau khi chiuẩn hóa có dạng \(\psi=\frac{1}{\sqrt{\pi32.a_0^5}}x.e^{-\frac{r}{2a_0}}\)


Đáp án C
Ta có: MX = 100: C5H8O2 Þ Các công thức cấu tạo của X là
HCOOCH=CH-CH2-CH3 ; HCOOCH=C(CH3)2 ; CH3COOCH=CH-CH3 ; C2H5COOCH=CH2.