K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 10 2021
\(a,B=4x^2+20x+25-9+x^2+14=5x^2+20x+30\\ b,B=5\left(x^2+4x+4\right)+10\\ B=5\left(x+2\right)^2+10\ge10>0,\forall x\)
Do đó B luôn dương với mọi x
29 tháng 10 2021
\(1,\\ a,=x^2-6x+8+3x^2-15x=4x^2-21x+8\\ b,=9x^2+12x+4-x^2+9=8x^2+12x+13\\ 2,\\ a,\Leftrightarrow x^2+8x+16-x^2+4=5\\ \Leftrightarrow8x=-15\Leftrightarrow x=-\dfrac{15}{8}\\ b,\Leftrightarrow9x^2-6x+1-8x^2-2x+12x+3-x^2=5\\ \Leftrightarrow4x=1\Leftrightarrow x=\dfrac{1}{4}\)
H9
HT.Phong (9A5)
CTVHS
8 tháng 8 2023
\(A=\dfrac{1}{x^2+x}+\dfrac{1}{x^2+3x+2}+\dfrac{1}{x^2+5x+6}+\dfrac{1}{x+3}\) (ĐK: \(x\ne-1;x\ne0;x\ne-2;x\ne-3\))
\(A=\dfrac{1}{x\left(x+1\right)}+\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{x+3}\)
\(A=\dfrac{\left(x+2\right)\left(x+3\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}+\dfrac{x\left(x+3\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}+\dfrac{x\left(x+1\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}+\dfrac{x\left(x+1\right)\left(x+2\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)\(A=\dfrac{x^2+5x+6+x^2+3x+x^2+x+x^3+2x^2+x^2+2x}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{x^3+6x^2+11x+6}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{x^3+5x^2+6x+x^2+5x+6}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{x\left(x+5x+6\right)+\left(x^2+5x+6\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{\left(x^2+5x+6\right)\left(x+1\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{\left(x+1\right)\left(x+2\right)\left(x+3\right)}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(A=\dfrac{1}{x}\)
7 tháng 10 2021
c: Ta có: \(6x^2-\left(2x+5\right)\left(3x-2\right)\)
\(=6x^2-6x^2+4x-15x+10\)
=-11x+10
d: Ta có: \(2x\left(3x-1\right)-\left(x-3\right)\left(6x+2\right)\)
\(=6x^2-2x-6x^2-2x+18x+6\)
=14x+6
TN
2
14 tháng 8 2021
\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)
29 tháng 10 2021
\(a,A=4-4x+x^2+6x^2-8x-8+9x^2+12x+4\\ A=16x^2\\ b,x=-\dfrac{1}{2}\Leftrightarrow A=16\cdot\dfrac{1}{4}=4\)
29 tháng 10 2021
a: \(A=x^2-4x+4+9x^2-12x+4+2\left(3x^2+2x-6x-4\right)\)
\(=10x^2-16x+8+6x^2-8x-8\)
\(=16x^2-24x\)
b: \(A=16\cdot\dfrac{1}{4}-24\cdot\dfrac{-1}{2}=4+12=16\)
TN
3
13 tháng 8 2021
\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1}{\left(3y+3\right)^3}=\dfrac{1}{27y^3+81y^2+81y+27}\)
LN
13 tháng 8 2021
\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1^3}{\left(3y+3\right)^3}=\dfrac{1}{27\left(y^3+3y^2+3y+1\right)}\)
23 tháng 7 2021
c) Ta có: \(C=7\left(x-8\right)^2-9\left(x+3\right)^2+50\)
\(=7\left(x^2-16x+64\right)-9\left(x^2+6x+9\right)+50\)
\(=7x^2-112x+448-9x^2-54x-81+50\)
\(=-2x^2-166x-31\)
\(=-2\cdot\dfrac{1}{49}-166\cdot\dfrac{-1}{7}-31\)
\(=\dfrac{-359}{49}\)
g) Ta có: \(G=x^{17}-3x^{16}+3x^{15}-3x^{14}+...+3x\)
\(=x^{17}-x^{16}\left(x+1\right)+x^{15}\left(x+1\right)-x^{14}\left(x+1\right)+...+x\left(x+1\right)\)
\(=x^{17}-x^{17}-x^{16}+x^{16}+x^{15}-x^{15}-x^{14}+...+x^2+x\)
=x
=2
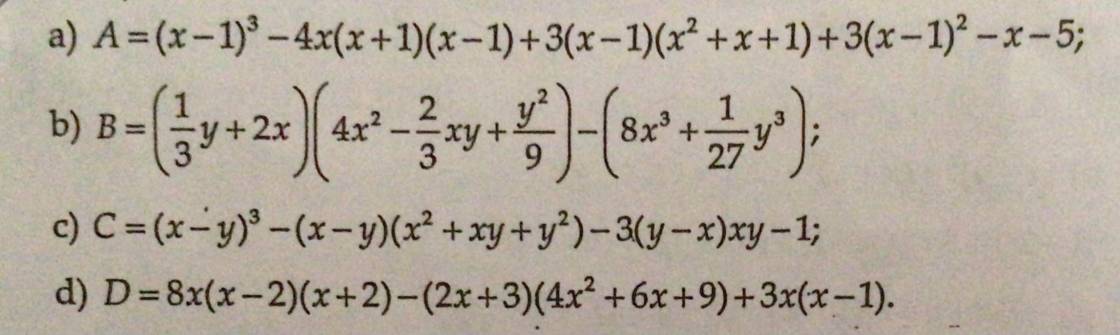
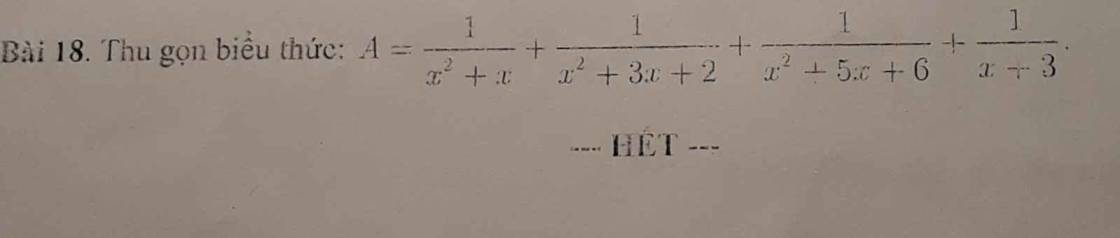
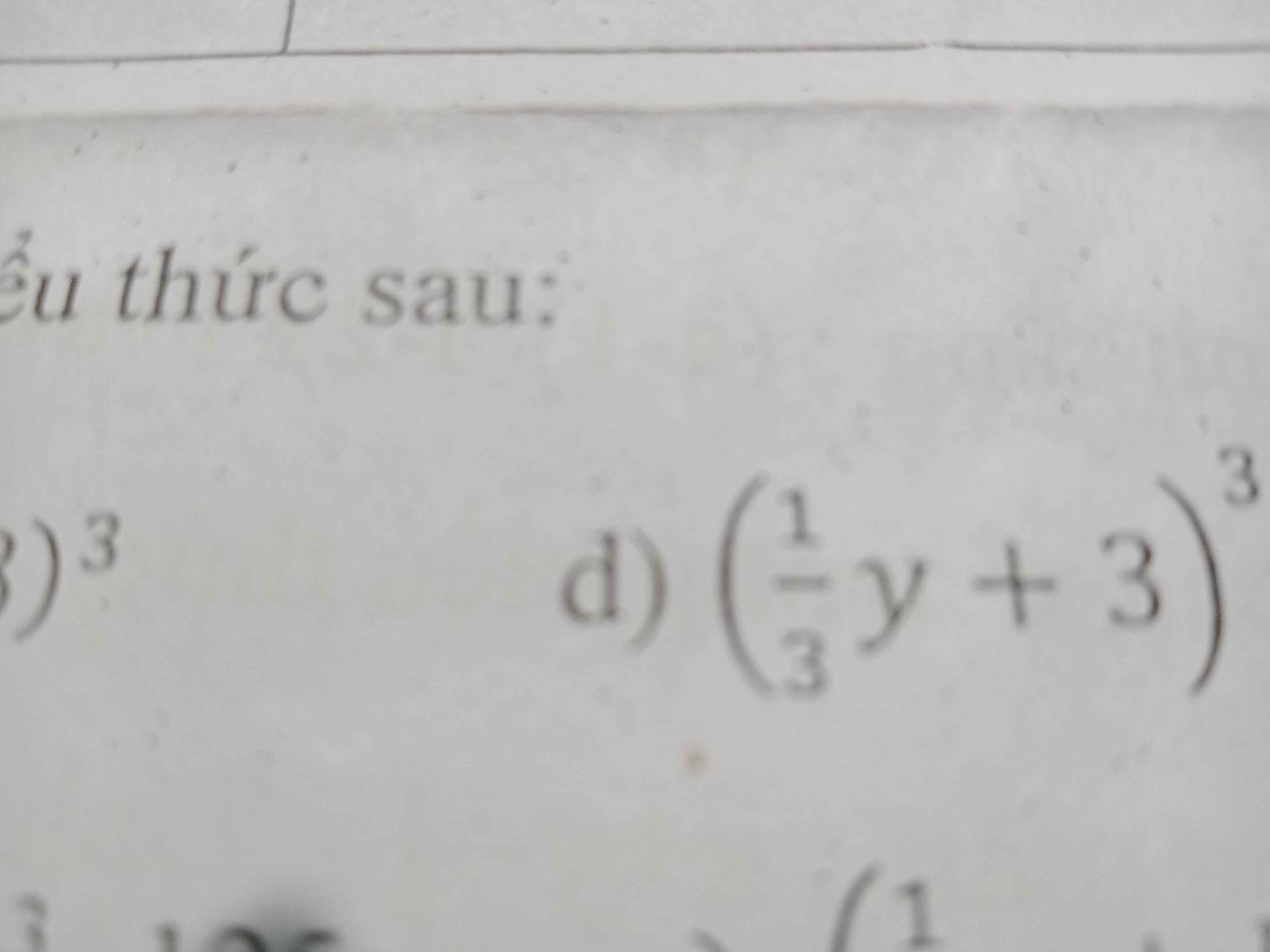
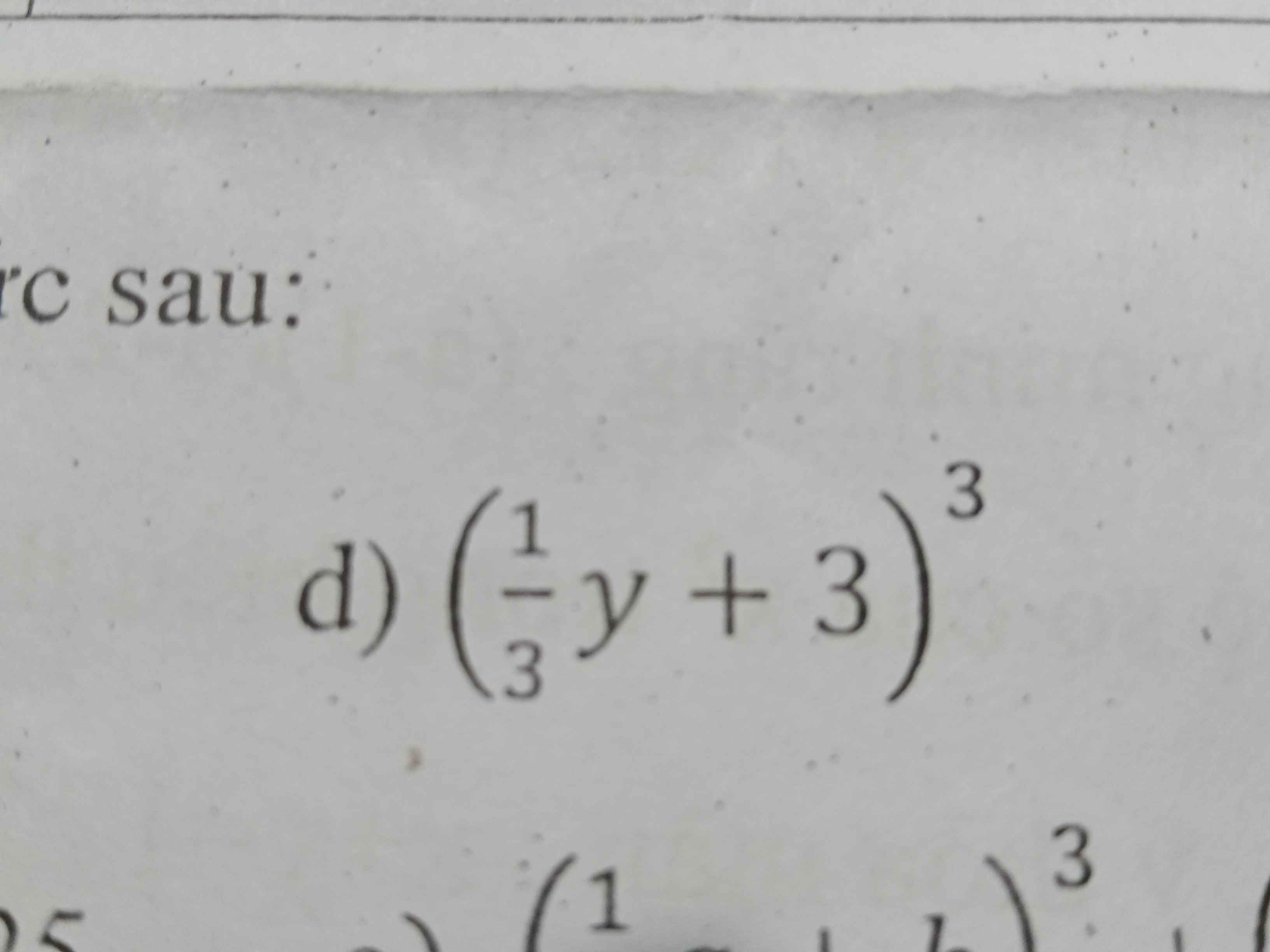
\(D=8x\left(x-2\right)\left(x+2\right)-\left(2x+3\right)\left(4x^2+6x+9\right)+3x\left(x-1\right)\\ =8x\left(x^2-4\right)-\left(2x+3\right)\left(2x+3\right)^2+3x\left(x-1\right)\\ =8x^3-32x-\left(2x+3\right)^3+3x^2-3x\\ =8x^3-32x-\left(8x^3+36x^2+54x+27\right)+3x^2-3x\\ =\left(8x^3-8x^3\right)-\left(36x^2-3x^2\right)-\left(32x+54x+3x\right)-27\\ =-33x^2+89x-27\)
\(B=\left(\dfrac{1}{3}y+2x\right)\left(4x^2-\dfrac{2}{3}xy+\dfrac{y^2}{9}\right)-\left(8x^3+\dfrac{1}{27}y^3\right)\\ =\left(\dfrac{1}{3}y+2x\right)\left[\left(2x\right)^2-2x.\dfrac{1}{3}y+\left(\dfrac{1}{3}y\right)^2\right]-\left[\left(2x\right)^3+\left(\dfrac{1}{3}y\right)^3\right]\\ =\left[\left(2x\right)^3+\left(\dfrac{1}{3}y\right)^3\right]-\left[\left(2x\right)^3+\left(\dfrac{1}{3}y\right)^3\right]\\ =0\)