LN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 1 2017
Theo đề ra , ta có : \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) ; Mà : \(a+2b+3c=44,2\)
\(\Rightarrow\frac{a}{3}=\frac{2b}{8}=\frac{3c}{15}\) . Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{3}=\frac{2b}{8}=\frac{3c}{15}=\frac{a+2b+3c}{3+8+15}=\frac{44,2}{26}=1,7\)
\(\Rightarrow\frac{a}{3}=1,7\Rightarrow a=1,7.3=5,1\)
\(\Rightarrow\frac{2b}{8}=1,7\Rightarrow b=1,7.8\div2=6,8\)
\(\Rightarrow\frac{3c}{15}=1,7\Rightarrow c=1,7.15\div3=8,5\)
\(\Rightarrow a+b-c=5,1+6,8-8,5=3,4\)
Vậy : a + b - c = 3,4
AT
3 tháng 1 2017
Theo đề bài ta có:
\(\frac{a}{3}=\frac{b}{5}\) và 3a - b = 17,2
Áp dụng t/c của dãy tỉ số = nhau ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{3a}{9}=\frac{3a-b}{9-5}=\frac{17,2}{4}=\frac{43}{10}=4,3\)
=> \(\left[\begin{matrix}a=4,3.3\\b=4,3.5\end{matrix}\right.\Rightarrow\left[\begin{matrix}a=12,9\\b=21,5\end{matrix}\right.\)
=> a + b = 12,9 + 21,5 = 34,4
Vậy giá trị của a + b = 34,4
3 tháng 1 2017
Theo bài ra ta có: \(3a-b=17,2\)
\(\frac{a}{b}=\frac{3}{5}\Rightarrow\frac{a}{3}=\frac{b}{5}\Rightarrow\frac{3a}{9}=\frac{b}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{3a}{9}=\frac{b}{5}=\frac{3a-b}{9-5}=\frac{17,2}{4}=4,3\)
\(\Rightarrow\left\{\begin{matrix}\frac{3a}{9}=4,3\Rightarrow a=\frac{4,3\cdot9}{3}=12,9\\\frac{b}{5}=4,3\Rightarrow b=4,3\cdot5=21,5\end{matrix}\right.\)
Khi đó \(a+b=12,9+21,5=34,4\)
9 tháng 2 2017
Ta có: x + y = 8
x + z = 10
y + z = 12
\(\Rightarrow x+y+x+z+y+z=8+10+12\)
\(\Rightarrow2x+2y+2z=30\)
\(\Rightarrow2\left(x+y+z\right)=30\)
\(\Rightarrow x+y+z=15\)
+) x + y = 8 \(\Rightarrow z=7\)
+) \(x+z=10\Rightarrow y=5\)
+) \(y+z=12\Rightarrow x=3\)
Vậy bộ số \(\left(x;y;z\right)\) là \(\left(3;5;7\right)\)
NY
11 tháng 11 2016
? nhưng lần sau thì kiếm người ns chuyện ở chỗ khác chứ đưg đăng lên đây nghe bn?
17 tháng 3 2018
dễ mà bạn những câu này trong sách giáo khoa chỉ rõ mà, bạn phải cố gắng suy nghĩ đi không hiểu có thể hỏi thầy cô nhé !!
3 tháng 1 2017
Theo bài ra ta có: \(2a+b=-6\)
\(\frac{a}{b}=\frac{-2,4}{3,8}\Rightarrow\frac{a}{-2,4}=\frac{b}{3,8}\Rightarrow\frac{2a}{-4,8}=\frac{b}{3,8}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{2a}{-4,8}=\frac{b}{3,8}=\frac{2a+b}{\left(-4,8\right)+3,8}=\frac{-6}{-1}=6\)
\(\Rightarrow\left\{\begin{matrix}\frac{2a}{-4,8}=6\Rightarrow a=\frac{6\cdot\left(-4,8\right)}{2}=-14,4\\\frac{b}{3,8}=6\Rightarrow b=6\cdot3,8=22,8\end{matrix}\right.\)
Khi đó \(a+b=-14,4+22,8=8,4\)
LH
19 tháng 4 2017
Căn cứ vào tháng sinh của các bạn trong lớp của mình để tìm tần số tương ứng. Sau đó điền kết quả vào bảng. Chẳng hạn điều tra tháng, năm sinh của một lớp tại một trường trung học cơ sở, ta có bảng thống kê số liệu ban đầu như sau:
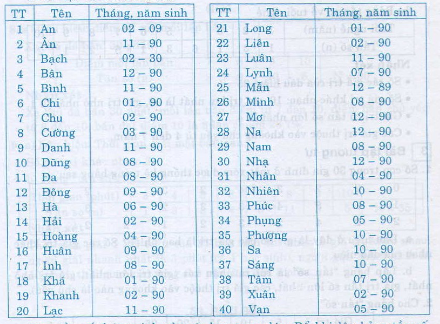
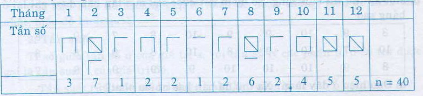
Tìm tần số tháng sinh của các bạn trong lớp. Để khi lập bảng tần số không nhần lẫn, ta kê ra tất cả các giá trị khác nhau của dấu hiệu (các tháng từ 1 - 12) lần lượt đọc tháng sinh từ trên xuống. Mỗi lần gặp tháng nào ta gạch vào cột tháng đó một vạch. Sau khi vạch xong, ta đếm số vạch của mỗi cột để ghi thành bảng "tần số" như sau:
YD
2
2 tháng 1 2017
=> \(\frac{5}{x}=\frac{1}{8}-\frac{y}{4}\)
=>\(\frac{5}{x}=\frac{1}{8}-\frac{2y}{8}\)
=>\(\frac{5}{x}=\frac{1-2y}{8}\)
=>5.8=(1-2y)x
=>40=(1-2y)x
Mà 2y là số chẵn nên 1-2y là số lẻ. => 1-2y\(\in\left\{1;-1;5;-5\right\}\)
=>2y\(\in\left\{0;2;-4;6\right\}\)
=>y\(\in\left\{0;1;-2;3\right\}\)
Lại có x và y là hai số tự nhiên nên y chỉ có thể bằng 0;1 hoặc 3
Thay y = 0 vào ta đc x =40
Thay y=1 vào ta đc x =-40
Thay y=3 vào ta đc x =-8
HT
0
AT
2 tháng 4 2017
Tính:
M = \(2334556\cdot321432543\)
\(=2334556\cdot\left(321\cdot10^6+432\cdot10^3+543\right)\)
\(=2334556\cdot321\cdot10^6+2334556\cdot432\cdot10^3+2334556\cdot543\)
\(=749392476000000+1008528192000+1267663908\)
\(=750402271855908\)
Tìm dư của phép chia: \(2006^{12}:33\)
Ta có: \(2006^2\equiv16\left(mod33\right)\)
\(\left(2006^2\right)^6\equiv16^6\equiv16\left(mod33\right)\)
Vậy dư của phép chia \(2006^{12}:33\) là 16
Lời giải:
$\sqrt[3]{27x+27}+\sqrt[3]{8x+8}=5$
$\sqrt[3]{27(x+1)}+\sqrt[3]{8(x+1)}=5$
$\sqrt[3]{27}.\sqrt[3]{x+1}+\sqrt[3]{8}.\sqrt[3]{x+1}=5$
$3\sqrt[3]{x+1}+2\sqrt[3]{x+1}=5$
$5\sqrt[3]{x+1}=5$
$\sqrt[3]{x+1}=1$
$x+1=1$
$x=0$