K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 10 2015
\(y'=1-\frac{3x^2}{\left(x^3\right)^2}=1-\frac{3}{x^4}\)
18 tháng 12 2016
\(\int\frac{2^{x-1}}{e^x}dx=\frac{1}{2}\int\left(\frac{2}{e}\right)^xdx=\frac{1}{2}.\frac{\left(\frac{2}{e}\right)^x}{ln\left(\frac{2}{e}\right)}+C=\frac{2^x}{2e^x\left(ln2-1\right)}+C\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 5 2020
Bài 1:
\(F'\left(x\right)=e^x+\left(x-1\right)e^x=xe^x=\frac{x}{e^x}.e^{2x}\Rightarrow f\left(x\right)=\frac{x}{e^x}\)
Xét \(I=\int f'\left(x\right)e^{2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{2x}\\v=f'\left(x\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2e^{2x}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I=f\left(x\right).e^{2x}+2\int f\left(x\right).e^{2x}dx=x.e^x+2\left(x-1\right)e^x+C=\left(3x-2\right)e^x+C\)
2.
Xét \(J=\int\limits^1_0xf\left(6x\right)dx\)
Đặt \(6x=t\Rightarrow dx=\frac{1}{6}dt\Rightarrow J=\frac{1}{36}\int\limits^6_0t.f\left(t\right)dt=\frac{1}{36}\int\limits^6_0x.f\left(x\right)dx=1\)
\(\Rightarrow I=\int\limits^6_0x.f\left(x\right)dx=36\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\frac{1}{2}x^2\end{matrix}\right.\)
\(\Rightarrow I=\frac{1}{2}x^2f\left(x\right)|^6_0-\frac{1}{2}\int\limits^6_0x^2.f'\left(x\right)dx\)
\(\Leftrightarrow36=18-\frac{1}{2}\int\limits^6_0x^2f'\left(x\right)dx\)
\(\Rightarrow\int\limits^6_0x^2f'\left(x\right)dx=-36\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 10 2019
\(f'\left(x\right)=0\) có 2 nghiệm bội lẻ \(x=0\) ; \(x=3\)
Mặt khác do hệ số của x trong \(3-x\) trái dấu hệ số của x nên nghiệm lớn hơn là điểm cực đại, nghiệm nhỏ hơn là điểm cực tiểu hay \(x=0\) là điểm cực tiểu
18 tháng 10 2015
=\(\sqrt{4x^2-3x-1}'=\left(\left(4x^2-3x-1\right)^{\frac{1}{2}}\right)'=\frac{1}{2}\left(4x^2-3x-1\right)'\left(4x^2-3x-1\right)^{\frac{1}{2}-1}=\frac{1}{2}\left(8x-3\right)\frac{1}{\sqrt{4x^2-3x-1}}\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 10 2020
Hàm \(x^x\) vừa là hàm mũ, vừa là hàm lũy thừa nên nó phải tuân theo điều kiện của cả 2 hàm này, tức là cơ số \(x>0\) chứ
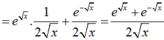
đạo hàm theo ẩn nào vậy bn
x