
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Điều kiện: x > 2.
Với điều kiện trên , phương trình đã cho trở thành:
x - 3 = x - 3 ⇔ x - 3 ≥ 0 ⇔ x ≥ 3
Kết hợp điều kiện, tập nghiệm của phương trình là S = [ 3 ; + ∞ )

Ta có: 2 x + 1 > 3 x - 2 - x - 3 < 0 ⇔ - x > - 3 - x < 3 ⇔ x < 3 x > - 3 ⇔ - 3 < x < 3

Ta có:
x - 3 x ≤ 0 ⇔ x 1 - 3 x ≤ 0 ⇔ [ x = 0 x > 0 1 - 3 x ≤ 0 ⇔ [ x = 0 x > 0 3 x ≥ 1 ⇔ [ x = 0 x > 0 x ≥ 1 3 ⇔ [ x = 0 x > 0 x ≥ 1 9 ⇔ [ x = 0 x ≥ 1 9

+ Khi m = 0, bất phương trình trở thành - 2 x + 2 < 0 ⇔ x > 1 . Vậy m = 0 không thỏa mãn yêu cầu của bài toán.
+ Khi m ≠ 0 , bất phương trình vô nghiệm khi m x 2 + 2 m - 1 x + m + 2 ≥ 0 , ∀ x ∈ ℝ . ⇔ a > 0 ∆ ' ≤ 0 ⇔ m > 0 ( m - 1 ) 2 - m ( m + 2 ) ≤ 0 .
⇔ m > 0 - 4 m + 1 ≤ 0 ⇔ m > 0 m ≥ 1 4 ⇔ m ≥ 1 4
Chọn C.

Vì \(x_2\)là nghiệm của phương trình
=> \(x_2^2-5x_2+3=0\)
=> \(x_2+1=x^2_2-4x_2+4=\left(x_2-2\right)^2\)
Theo viet ta có
\(\hept{\begin{cases}x_1+x_2=5\\x_1x_2_{ }=3\end{cases}}\)=> \(x_1^2+x_2^2=19\)
Khi đó
\(A=||x_1-2|-|x_2-2||\)
=> \(A^2=\left(x^2_1+x_2^2\right)-4\left(x_1+x_2\right)+8-2|\left(x_1-2\right)\left(x_2-2\right)|\)
=> \(A^2=19-4.5+8-2|3-2.5+4|=1\)
Mà A>0(đề bài)
=> A=1
Vậy A=1

a, Mệnh đề đúng
\(\Rightarrow \overline P:\)\(\sqrt{3}+\sqrt{2}\ne\frac{1}{\sqrt{3}-\sqrt{2}}\)
b, Mệnh đề sai
\(\Rightarrow \overline P:\) \(\left(\sqrt{2}-\sqrt{18}\right)^2\le8\)
c, Mệnh đề đúng
\(\Rightarrow \overline P:\) \(\left(\sqrt{3}+\sqrt{12}\right)^2\) không là một số hữu tỉ
d, Mệnh đề đúng
\(\Rightarrow \overline P:\) x = 2 không là nghiệm của PT \(\frac{x^2-4}{x-1}=0\)
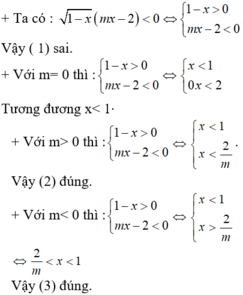
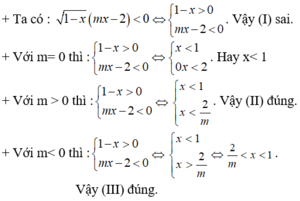
Ta có: x 2 - 6 2 x + 18 = x - 3 2 2 ≥ 0 ∀ x
Tập nghiệm của bất phương trình x 2 - 6 2 x + 18 ≥ 0 là S= R.