Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có \(log^{27}_2=log^{3^3}_2=3log^3_2=a\Rightarrow log^3_2=\frac{a}{3}\)
mặt khác
\(log^{\sqrt[6]{2}}_{\sqrt{3}}=\frac{1}{log^{\sqrt{3}}_{\sqrt[6]{2}}}=\frac{1}{log^{3^{\frac{1}{2}}}_{2^{\frac{1}{6}}}}=\frac{1}{\frac{1}{2}log^3_{2^{\frac{1}{6}}}}=\frac{1}{\frac{1}{2}\frac{1}{\frac{1}{6}}log_2^3}=\frac{1}{3.log_2^3}=\frac{1}{3}.\frac{a}{3}=\frac{a}{9}\)

a) \(4x-7>0\Leftrightarrow4x>7\)\(\Leftrightarrow x>\frac{7}{4}\)
b) \(-5x+8>0\Leftrightarrow5x<8\Leftrightarrow x<\frac{8}{5}\)
c)\(9x-10\le0\Leftrightarrow9x\le10\)\(\Leftrightarrow x\le\frac{10}{9}\)
d) \(\left(x+1\right)^2+4\le x^2+3x+10\)\(\Leftrightarrow x^2-2x+1+4\le x^2+3x+10\)
\(\Leftrightarrow5x\ge-5\Leftrightarrow x\ge-1\)
a,
4x - 7 > 0
↔ 4x > 7
↔ x > \(\dfrac{7}{4}\)
Vậy tập nghiệm của bất phương trình là S = { x / x>\(\dfrac{7}{4}\) }
b,
-5x + 8 > 0
↔ 8 > 5x
↔ \(\dfrac{8}{5}\) > x
Vậy tập nghiệm của bất phương trình là S = { x / \(\dfrac{8}{5}\) > x }
c,
9x - 10 ≤ 0
↔ 9x ≤ 10
↔ x ≤ \(\dfrac{10}{9}\)
Vậy tập nghiệm của bất phương trình là S = { x / x ≤ \(\dfrac{10}{9}\) }
d,
( x - 1 )\(^2\) + 4 ≤ x\(^2\) + 3x + 10
↔ x\(^2\) - 2x +1 +4 ≤ x\(^2\) + 3x + 10
↔ 1 + 4 - 10 ≤ x \(^2\) - x\(^2\) + 3x + 2x
↔ -5 ≤ 5x
↔ -1 ≤ x
Vậy tập nghiệm của bất phương trình là S = { x / -1 ≤ x}

\(\sqrt{x+2}-\sqrt{x-6}>2\)(ĐK: x\(\ge\)6)
\(\Leftrightarrow\sqrt{x+2}>2+\sqrt{x-6}\)
\(\Leftrightarrow x+2>4+4\sqrt{x-6}+x-6\)
\(\Leftrightarrow4>4\sqrt{x-6}\)
<=>\(1>\sqrt{x-6}\)
<=>1>x-6
<=>x<7 Mà x\(\ge\)6 =>x=6

a: \(F\left(x\right)=x^4+6x^3+2x^2+x-7\)
\(G\left(x\right)=-4x^4-6x^3+2x^2-x+6\)
b: h(x)=f(x)+g(x)
\(=x^4+6x^3+2x^2+x-7-4x^4-6x^3+2x^2-x+6\)
\(=-3x^4+4x^2-1\)
c: Đặt h(x)=0
\(\Leftrightarrow3x^4-4x^2+1=0\)
\(\Leftrightarrow\left(3x^2-1\right)\left(x^2-1\right)=0\)
hay \(x\in\left\{1;-1;\dfrac{\sqrt{3}}{3};-\dfrac{\sqrt{3}}{3}\right\}\)
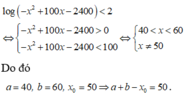


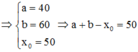
Đáp án C