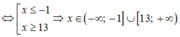Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để dấu tam thức không đổi trên R
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\\Delta'< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\36+5m< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m< -\frac{36}{5}\end{matrix}\right.\)
\(\Rightarrow m< -\frac{36}{5}\)

a)
\(\Delta=9-20=-11\) vô nghiêm
=> A luôn dương (+) với mọi x thuộc R
b) {a-b+c=0}
B= 0 khi x= -1 hoặc x= 5/2
B>0 khi -1<x<5/2
B<0 khi x<-1 hoặc x>/52
c) x^2 +12x+36 =(x+6)^2
C = 0 khi x =-6
C > 0 mọi x khác -6
d)
D = 0 khi x =3/2 hoặc x=-5
D> 0 khi x<-5 hoặc x>3/2
D<0 khi -5<x<3/2

\(f\left(x\right)>0;\forall x\)
\(\Leftrightarrow\Delta'=1+3m< 0\Rightarrow m< -\frac{1}{3}\)

a) F(x) = \(-x^2\left(x-1\right)\left(x+2\right)\left(x+2\right)=\left(1-x\right)x^2\left(x+2\right)^2\\ \)
\(\left\{{}\begin{matrix}x^2\ge0\\\left(x+2\right)^2\ge0\end{matrix}\right.\) => dấu biểu thức chỉ phụ thuộc vào thừa số (1-x)
F(x) =0 khi x={-2,0,1}
F(x) > 0 khi x<1 và khác -2 và 0
f(x) <0 khi x> 1
Tử f(x) =x^2(x^2-3x+2) =x^2(x-1)(x-2)
tương tự a) dấu của tử phụ thuộc (x-1)(x-2)
Mẫu f(x) =x^2 -x-30 =(x-5)(x+6)
Phần hỗ trợ Lập bảng đây khó thao tác
=> viết bằng hệ {điểm tới hạn xet x={-6,0,1,2,5}
Khi => \(\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)=>f(x) =0
Khi \(\left[{}\begin{matrix}x=5\\x=-6\end{matrix}\right.\) => f(x) không xác định
Khi \(x< -6\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)>0\end{matrix}\right.\)\(\Rightarrow f\left(x\right)>0\)
khi -6<x<1 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) <0
khi 1<x<2 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)< 0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) >0
khi 2<x<5 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) <0
khi x>5 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)>0\end{matrix}\right.\) => f(x) >0

1/ \(y=x^2-2x-3=\left(x-1\right)^2-4\)
\(\left(x-1\right)^2-4>0\) khi
\(\left(x-1\right)^2>4\Rightarrow x-1>2\Rightarrow x>3\)
2/ \(y=x^2-3x-4=\left(x-\dfrac{3}{2}\right)^2-\dfrac{25}{4}\)
\(y>0\) khi
\(\left(x-\dfrac{3}{2}\right)^2>\dfrac{25}{4}\Rightarrow x-\dfrac{3}{2}>\dfrac{5}{2}\Rightarrow x>4\)
Chọn D.
Tam thức bậc hai f(x) = x 2 - 12x - 13 nhận giá trị không âm khi và chỉ khi
f(x) ≥ 0 ⇔ x 2 - 12x - 13 ≥ 0