Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: AH=12cm
c: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
Suy ra: AM=AN
d: Xét ΔABC có AM/AB=AN/AC
nên MN//BC

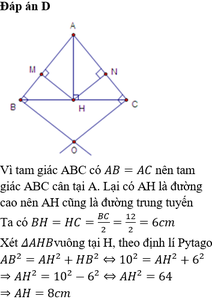
\(\text{a) Có }\Delta ABC\text{cân tại A}\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\text{Xét }\Delta AHB\text{ và }\Delta AHC\text{ có:}\)
\(\widehat{AHB}=\widehat{AHC}=90^o\)
\(AB=AC=10cm\)\(\Rightarrow\)\( \Delta AHB\text{=}\Delta AHC\left(ch-gn\right)\)
\(\widehat{ABC}=\widehat{ACB}\)
\(\text{b) Có }\Delta AHB=\Delta AHC\Rightarrow HB=HC=\frac{BC}{2}=\frac{12}{2}=6\left(cm\right)\)
\(\text{ Xét }\Delta AHB\text{vuông tại H có:}\)
\(AH^2+BH^2=AB^2\) (Định lý py-ta-go)
\(AH^2=AB^2-BH^2=10^2-6^2=100-36=64\)
\(AH=\sqrt{64}=8\left(cm\right)\)
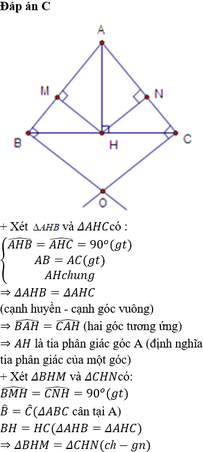
\(\text{c) Xét }\Delta BHM\text{ và }\Delta CHN\text{ có:}\)
\(\widehat{BMH}=\widehat{CNH}=90^o\)
\(HB=HC\text{ (CMT)}\)\(\Rightarrow\)\(\text{ }\Delta BHM\text{ = }\Delta CHN \left(CH-GN\right)\)
\(\widehat{ABC}=\widehat{ACB}\)
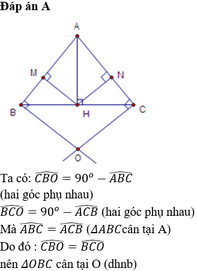
\(\text{d) }\)\(\text{Ta có: }MH\perp AB,OB\perp AB\Rightarrow MH//OB\)
\(\Rightarrow\widehat{MHB}=\widehat{CBO}\text{ (2 góc so le trong)}\)
\(\text{Ta có: }NH\perp AC,OC\perp AC\Rightarrow NH//OC\)
\(\Rightarrow\widehat{NHC}=\widehat{BCO}\text{ (2 góc so le trong)}\)
\(\text{ }\text{Mà }\Delta BHM\text{ = }\Delta CHN\Rightarrow\widehat{MHB}=\widehat{NHC}\)
\(\text{Hay}\widehat{CBO}=\widehat{BCO}\)\(\Rightarrow\Delta OBC\text{ cân tại O}\)

a. △ABC cân tại A, lại có AH là đường cao
=> AH cũng là đường trung tuyến; đường phân giác
=> HB = HC
áp dụng định lý pythagore vào △ABH vuông tại B ta có:

b. xét △ vuông AMH và △ vuông ANH có
AH cạnh chung; góc MAH = góc NAH (câu a)
=> △ AMH = △ANH (ch-gn)
=> HM = HN (2 cạnh tương ứng)
△ AMH = △ANH (câu b) => AM = AN
=> △AMN là △ cân tại A
xét △AMN có: \(\widehat{AMN}=\dfrac{180^0-\widehat{A}}{2}\left(1\right)\)
xét △ABC có: \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\left(2\right)\)
TỪ (1) (2) \(=>\widehat{AMN}=\widehat{ABC}\)
mà 2 góc này ở vị trí đồng vị
=> MN // BC
c. ta có MN // BC (câu B) (3)
vì MK ⊥ BC và NP ⊥ BC
=> MK // NP (4)
từ (3) (4) => tứ giác MNPK là HCN
=> MN = KP
Help me