Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Có AH2=HF.HD \(\rightarrow\)\(\frac{AH}{HF}=\frac{HD}{AH}\)
Xét \(\Delta\)AHD và \(\Delta\)FHA có:
\(\widehat{AHD}=\widehat{FHA}=90^o\)
\(\frac{AH}{HF}=\frac{HD}{AH}\)( chứng minh trên)
\(\rightarrow\Delta\)AHD\(\approx\)\(\Delta\)FHA (c-g-c)
\(\rightarrow\)\(\widehat{ADH}=\widehat{FAH}\)( 2 góc tương ứng)
mà \(\widehat{ADH}+\widehat{HAD}=90^o\)
nên \(\widehat{FAH}+\widehat{HAD}=90^o\)
hay \(\widehat{FAD}=90^o\)\(\rightarrow\Delta\)ADF vuông tại A
A B C D E F H
Gợi ý: EF // BC => EF vuông AH
Áp dụng định lí Pitago
\(BE^2=AB^2+BE^2=BD^2+DE^2\)
=> \(\left(BH^2+AH^2\right)+\left(AF^2+FE^2\right)=\left(BH^2+HD^2\right)+\left(EF^2+FD^2\right)\)
=> \(HA^2+AF^2=HD^2+FD^2\)
=> \(\left(AF+FH\right)^2+AF^2=HD^2+\left(HD+FH\right)^2\) ( dùng hằng đẳng thức và rút gọn)
=> \(AF^2+AF.FH=HD^2+HD.FH\)
=> \(\left(AF^2-HD^2\right)+FH\left(AF-HD\right)=0\)
=> AF=HD
a) Vì \(\frac{CD}{AC}=\frac{1,5}{3}=\frac{1}{2}\); \(\frac{CE}{BC}=\frac{2,5}{5}=\frac{1}{2}\)
Nên \(\frac{CD}{AC}=\frac{CE}{BC}=\frac{1}{2}\)
Xét ΔCDE và ΔCAB có
\(\frac{CD}{AC}=\frac{CE}{BC}=\frac{1}{2}\)
Góc DCE=ACB(đối đỉnh)
Vậy hai tam giác đồng dạng với nhau
=> Góc CDE=CAB=90 độ
Vậy ΔCDE là tam giác vuông.
Áp dụng định lí Pi-ta-go vào ΔCDE ta có:
\(CE^2=DC^2+DE^2\Rightarrow DE^2=CE^2-CD^2=2,5^2-1,5^2=4\)
=> \(DE=\sqrt{4}=2cm\).
b) Vì ΔCDE đồng dạng với ΔCAB nên
\(\frac{CD}{AC}=\frac{DE}{AB}\Rightarrow AB=\frac{AC.DE}{CD}=\frac{3.2}{1,5}=4\left(cm\right)\)
ΔABC vuông tại A, đường cao AH, theo hệ thức lượng, ta có:
- \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{4.3}{5}=2,4\left(cm\right)\)
- \(AC^2=CH.BC\Rightarrow CH=\frac{AC^2}{BC}=\frac{3^2}{5}=\frac{9}{5}=1,8\left(cm\right)\)
\(CH=BC-CH=5-1,8=3,2\left(cm\right)\)
câu d:
Tam giác BCF nội tiếp (O;BC/2) có cạnh BC là đường kính
=> Tam giác BCF vuông tại F
=>góc BFC=90 độ
Xét 2 tam giác: tam giác CHF và tam giác CFB có:
góc C chung
góc CHF=góc CFB (=90 độ)
Do đó, tam giác CHF đồng dạng với tam giác CFB (g.g)
=> góc CFH=góc CBF (1)
Tứ giác ABFC nội tiếp (O;BC/2)
=> góc CFH=góc ABC (cùng chắn cung AC) (2)
Từ (1) và (2)=> góc CBF=góc ABC (3)
Mà tia BC nằm giữa tia AB và BF (4)
Từ (3) và (4)=> BC là tia phận giác của góc ABF (đpcm)
GIẢI: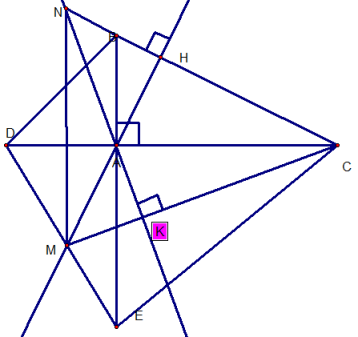
a) Xét Δ ABC và Δ AED, ta có :
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
=> AD 
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : 
=> BD // CE
b) Xét Δ MNC, ta có :
NK
MH
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN
mà : AB
=> MN // AB.
c) Xét Δ AMC, ta có :
=>
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
IM cạnh chung.
mặt khác : 
mà :
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.
a: góc CDM=1/2*sđ cung CM=90 độ
góc CAB=góc CDB=90 độ
=>ABCD nội tiếp
c: Gọi F là giao của AB và CD
góc MEC=1/2*sđ cung MC=90 độ
=>ME vuông góc CB(1)
Xet ΔFCB có
CA,BD là đường cao
CA cắt BD tại M
=>M là trực tâm
=>FM vuông góc BC(2)
Từ (1), (2) suy ra F,M,E thẳng hàng