
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(A + B + C = {180^0}\)(tổng 3 góc trong một tam giác)
\(\begin{array}{l} \Rightarrow A = {180^0} - \left( {B + C} \right)\\ \Leftrightarrow \sin A = \sin \left( {{{180}^0} - \left( {B + C} \right)} \right)\\ \Leftrightarrow \sin A = \sin \left( {B + C} \right) = \sin B.\cos C + \sin C.\cos B\end{array}\)

Ta có \sin 5\alpha -2\sin \alpha \left({\cos} 4\alpha +\cos 2\alpha \right)=\sin 5\alpha -2\sin \alpha .\cos 4\alpha -2\sin \alpha .\cos 2\alphasin5α−2sinα(cos4α+cos2α)=sin5α−2sinα.cos4α−2sinα.cos2α
=\sin 5\alpha -\left(\sin 5\alpha -\sin 3\alpha \right)-\left(\sin 3\alpha -\sin \alpha \right)=sin5α−(sin5α−sin3α)−(sin3α−sinα)
=\sin \alpha .=sinα.
Vậy \sin 5\alpha -2\sin \alpha \left({\cos} 4\alpha +\cos 2\alpha \right)=\sin \alphasin5α−2sinα(cos4α+cos2α)=sinα

Đkxđ: \(x\in R\).
\(cos2x-cos3x+cos4x=0\Leftrightarrow\left(cos2x+cos4x\right)-cos3x=0\)
\(\Leftrightarrow2cos3x.cosx-cos3x=0\)
\(\Leftrightarrow cos3x\left(2cos2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=0\\2cos2x-1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}cos3x=0\\cos2x=\dfrac{1}{2}\end{matrix}\right.\)
\(cos3x=0\Leftrightarrow3x=\dfrac{\pi}{2}+k\pi\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
\(cos2x=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
\(\dfrac{sinB}{sinC}=2cosA\Leftrightarrow sinB=2cosA.sinC\)
\(\Leftrightarrow sinB=sin\left(A+C\right)+sin\left(C-A\right)\)
\(\Leftrightarrow sinB=sin\left(\pi-\left(A+C\right)\right)+sin\left(C-A\right)\)
\(\Leftrightarrow sinB=sinB+sin\left(C-A\right)\)
\(\Leftrightarrow sin\left(C-A\right)=0\) (1)
Do A, C là số đo các góc trong tam giác nên từ (1) suy ra:
\(C=A\) hay tam giác ABC cân.

Xét các vec tơ đơn vị \(\frac{\overrightarrow{AB}}{AB};\frac{\overrightarrow{BC}}{BC};\frac{\overrightarrow{CA}}{CA}\) trên các cạnh AB, BC, CA của tam giác ABC
Có \(0\le\left(\frac{\overrightarrow{AB}}{AB};\frac{\overrightarrow{BC}}{BC};\frac{\overrightarrow{CA}}{CA}\right)^2=3-2\left(\cos A+\cos B+\cos C\right)\)
Suy ra \(\cos A+\cos B+\cos C\le\frac{3}{2}\) => Điều cần chứng minh

a) \(cos\left(A+B\right)+cosC=0\)
\(\Leftrightarrow cos\left(\pi-C\right)+cosC=0\)
\(\Leftrightarrow-cosC+cosC=0\)
\(\Leftrightarrow0=0\left(đúng\right)\)
\(\Leftrightarrow dpcm\)
b) \(cos\left(\dfrac{A+B}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{\pi-C}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{\pi}{2}-\dfrac{C}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow sin\dfrac{C}{2}=sin\dfrac{C}{2}\left(đúng\right)\)
\(\Leftrightarrow dpcm\)
c) \(cos\left(A-B\right)+cos\left(2B+C\right)=0\left(1\right)\)
Ta có : \(A+B+C=\pi\)
\(\Leftrightarrow2B+C=\pi-A+B\)
\(\Leftrightarrow2B+C=\pi-\left(A-B\right)\)
\(\left(1\right)\Leftrightarrow cos\left(A-B\right)+cos\left[\pi-\left(A-B\right)\right]=0\)
\(\Leftrightarrow cos\left(A-B\right)-cos\left(A-B\right)=0\)
\(\Leftrightarrow0=0\left(đúng\right)\)
\(\Leftrightarrow dpcm\)
THAM KHẢO:
Giải chi tiết:
Nếu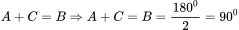 : Tam giác ABC vuông tại B.
: Tam giác ABC vuông tại B.
Nếu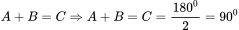 : Tam giác ABC vuông tại C.
: Tam giác ABC vuông tại C.
Vậy, tam giác ABC vuông tại B hoặc C.