Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M K F E N O
cau a:CB;AN là trung tuyến ;CB/MB=2/3
> M trọng tâm tam giác ACD > vậy A;M;N thẳng hàng
câu b:DM là đường trung tuyến thứ 3> K trung diemAC.
cậu c: tương tự AF;CE;MK đồng qui tại O là trọng tâm tam giác ACM

thực sự là mình không biết vẽ hình
Chứng minh
a, Xét \(\Delta ABE\) và \(\Delta DBE\) có
BE chung
\(\widehat{BAE}=\widehat{BDE}\) (=1v)
BA = BD (gt)
\(\Rightarrow\Delta ABE=\Delta DBE\left(ch-cgv\right)\)
b, \(\Delta ABE=\Delta DBE\) (câu a )
\(\Rightarrow\widehat{ABE}=\widehat{DBE}\) (hai gó tương ứng)
\(\Rightarrow EA=ED\) (hai cạnh tương ứng) (1)
mà \(\Delta EDC\) vuông tại D
\(\Rightarrow EC>ED\) (2)
Từ (1) và (2) \(\Rightarrow EC>EA\)
Gọi N là giao điểm của AD và BE
Xét \(\Delta ABN\) và \(\Delta DBN\) có :
BA = BD (gt)
\(\widehat{ABN}=\widehat{DBN}\) (c/m trên)
BN chung
\(\Rightarrow\Delta ABN=\Delta DBN\) (c.g.c)
\(\Rightarrow AN=ND\) (hai cạnh tương ứng) (3)
và \(\widehat{ANB}=\widehat{DNB}\) (hai góc tương ứng)
mà \(\widehat{ANB}+\widehat{DNB}=180^O\)
\(\Rightarrow\widehat{ANB}=\widehat{DNB}\) (=1v) (4)
Từ (3) và (4) \(\Rightarrow BE\) là đường trung trực của AD
a) xét 2 tam giac vuong ABE va DBE co
AB = BD (gt)
BE canh chung
suy ra: tam giac ABE = tam giac DBE (ch-cgv)
b) tu cau a) Tam giac ABE = tam giac DBE
Suy ra :AE = DE (2 canh tuong ung) (1)_
trong tam giác EDC vuông tại D
suy ra : EC > DE (canh huyen lon hon cach goc vuong ) (2)
Tu (1) va (2) suy ra: EC >EA
Ta co : AE=ED (cmt)
suy ra: E thuộc đường trung trực của AD (3)
ta có:AB=BD(gt)
suy ra: B thuoc duong trung truc AD (4)
tu (3) va (4) suy ra: BE la duong trung truc cua AD
A B C E D M

Này phạm nhất duy , chắc có lẽ bạn chưa học , nếu \(\Delta\)ABD cân ( vì AD = AB ) mà AK là đường phân giác của tam giác đó thì \(\Rightarrow\) AK là đường cao , đường trung tuyến , đường trung trực của \(\Delta\)ABD

A B C M H N K
a) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
AB = AC (\(\Delta ABC\) cân tại A)
AM chung
BM = CM (suy từ gt)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\)
b) Do \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
hay \(\widehat{HBM}=\widehat{KCM}\)
Xét \(\Delta HBM\) vuông tại H và \(\Delta KCM\) vuông tại K có;
BM = CM
\(\widehat{HBM}=\widehat{KCM}\) (c/m trên)
\(\Rightarrow\Delta HBM=\Delta KCM\left(ch-gn\right)\)
c) Ta có: \(BM=CM=\dfrac{1}{2}BC\) (M là tđ)
\(\Rightarrow BM=CM=\dfrac{1}{2}.16=8\)
Vì \(\Delta ABM=\Delta ACM\)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^o\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}\) = \(90^o\)
\(\Rightarrow\Delta ABM\) vuông tại M
Áp dụng định lý pytago vào \(\Delta ABM\) vuông tại M có:
\(AB^2=AM^2+BM^2\)
\(\Rightarrow AM^2=17^2-8^2\)
\(\Rightarrow AM^2=15^2\)
\(\Rightarrow AM=15\)
Lại có: \(AN=NM=\dfrac{1}{2}AM=\dfrac{1}{2}.15=7,5\)
Vậy \(S_{\Delta BNC}=\dfrac{NM.BC}{2}=\dfrac{7,5.16}{2}=60\) \(\left(cm^2\right)\).
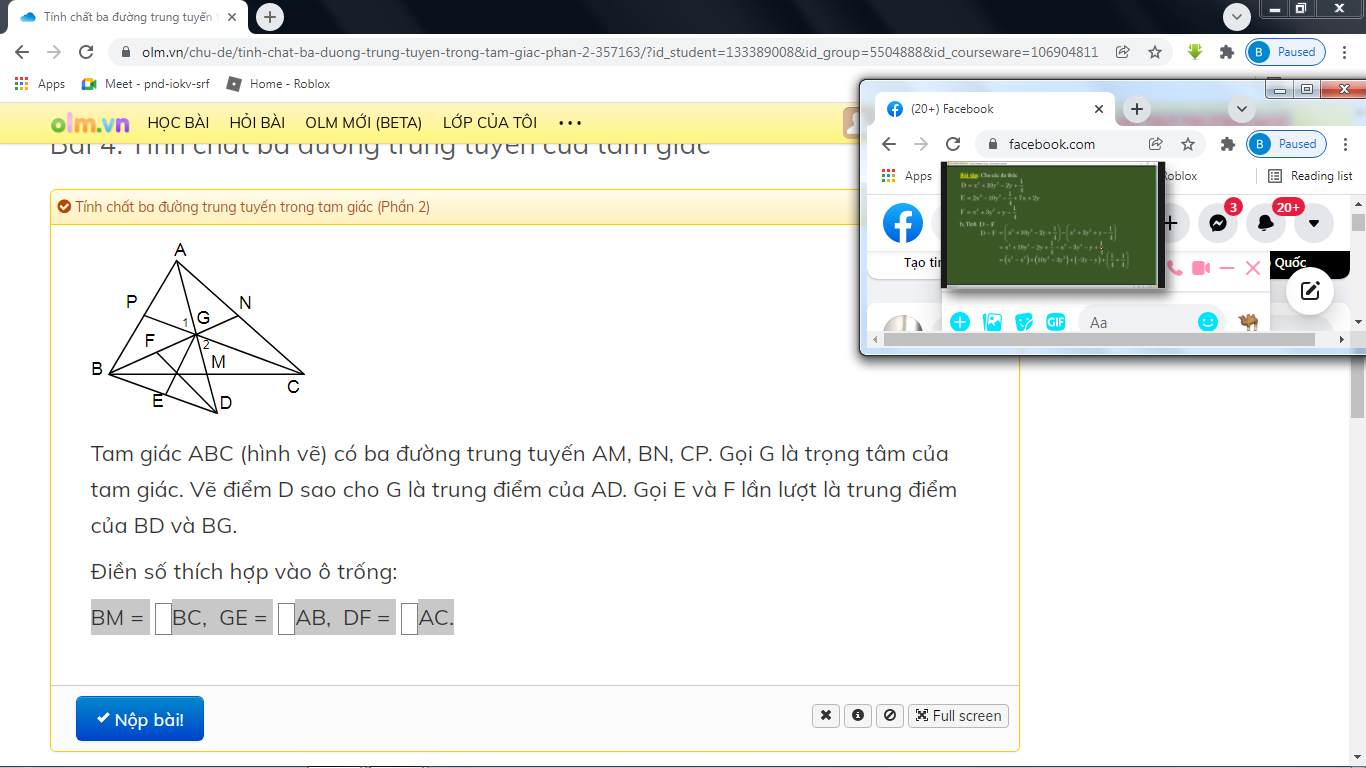
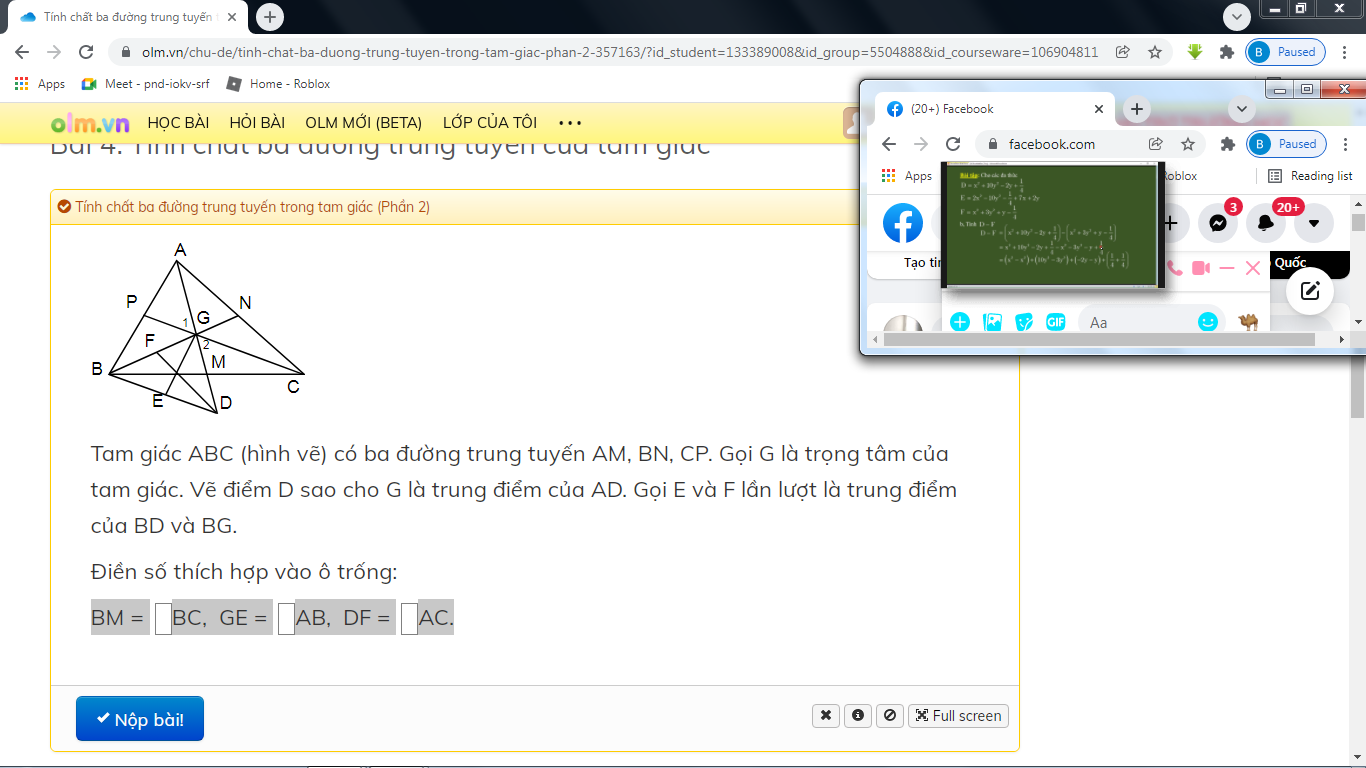
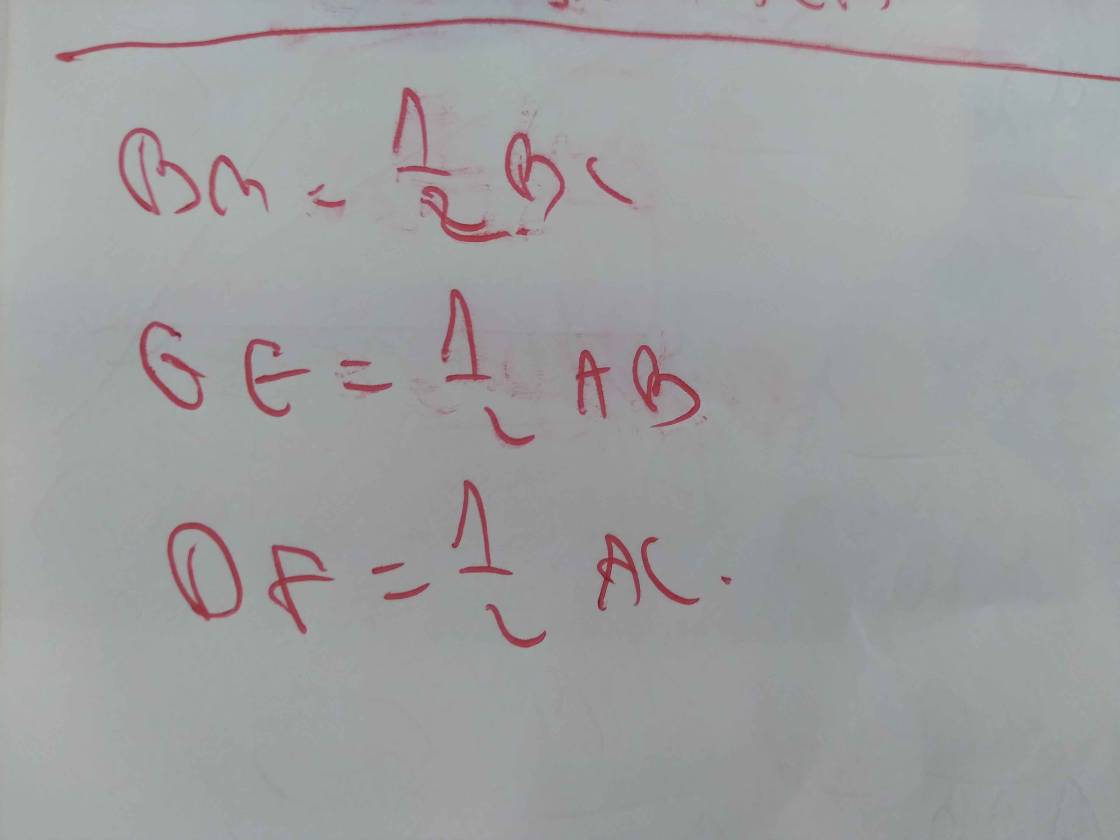

\(BM=\dfrac{1}{2}BC\)
\(GE=\dfrac{1}{2}AB\)
DF=AC