Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tg: EAB và tg DAC có :
AE = AD ( gt)
^A chung
AB = AC ( gt)
=> tg EAB = tg DAC ( c.g.c) => BE = CD; ^ABE = ^ACD ( cặp cạnh, góc tương ứng = nhau)
c) Xét tg BDC và tg CEB có:
BC chung
^DBC = ^ECB (gt)
BD =CE
=> tg BDC = tg ECB ( c.g.c) => ^BDC = ^CEB ( cặp góc tuong úng )
xét tg BDK và tg CEK có
^DBE = ^ ECD (cmt)
BD = CE
^BDC = ^CEB (cmt)
=> tg BDK = tg CEK ( g.c.g) => BK = CK => tg BKC cân tại K.

a: Xét ΔABE và ΔACDcó
AB=AC
góc BAE chung
AE=AD
=>ΔABE=ΔACD
=>BE=CD
b: ΔABE=ΔACD
=>góc ABE=góc ACD
c: góc ABE+góc KBC=góc ABC
góc ACD+góc KCB=góc ACB
mà góc ABE=góc ACD và góc ABC=góc ACB
nên góc KBC=góc KCB
=>KB=KC
d: AB=AC
KB=KC
=>AK là trung trực của BC
=>A,K,I thẳng hàng

a, Ta có : \(AD=AE\left(gt\right)\)
→ ΔADE là tam giác cân ở A
\(\Rightarrow\widehat{ADE}=\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}=\dfrac{180^0-40}{2}=70^0\)
Mà ΔABC cũng là tam giác cân
\(\Rightarrow\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}=70^0\)
\(\Rightarrow\widehat{ADE}=\widehat{ABC}\left(=70^0\right)\)
mà 2 góc này ở vị trí so le trong
\(\Rightarrow DE//BC\)
b, Xét ΔABE và ΔACD có :
\(AB=AC\left(\Delta ABC\cdot cân\right)\)
\(\widehat{A}:chung\)
\(AD=AE\left(gt\right)\)
\(\Rightarrow\Delta ABE=\Delta ACD\left(c-g-c\right)\)
c, Nối dài đoạn AI xuống BC, ta được đường phân giác AK của tam giác ABC.
Mà ΔABC cân ở A
→ AK là đường trung tuyến của tam giác ABC
→ AI cũng là đường trung tuyến của tam giác ABC

Cho tam giác ABC cân tại A lấy điểm D trên cánh AC điểm trên canh AC sao cho BD bằng CE
a chứng minh rằng AD bằng AE và hai tam giác ABE bằng hai tam giác AcD
b chúng minh rằng AI là đường phân giác của góc BAC

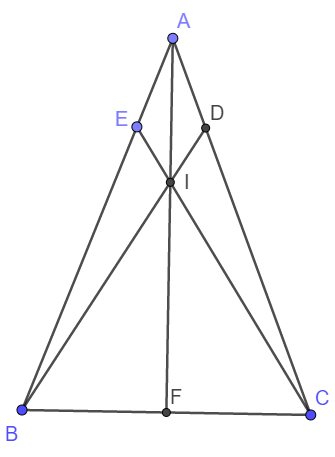
a) Xét tam giác ADB và AEC có:
AD = AE (gt)
AB = AC (gt)
Góc A chung
\(\Rightarrow\Delta ADB=\Delta AEC\left(c-g-c\right)\Rightarrow BD=CE\)
b) Do AB = AC; AD = AE nên BE = DC
Xét tam giác CEB và BDC có:
CE = BD (cma)
Cạnh BC chung
BC = CD (cmt)
\(\Rightarrow\Delta CEB=\Delta BDC\left(c-c-c\right)\)
c) Do \(\Delta ADB=\Delta AEC\Rightarrow\widehat{EBI}=\widehat{DCI}\)
Do \(\Delta CEB=\Delta BDC\Rightarrow\widehat{BEI}=\widehat{CDI}\)
Xét tam giác BIE và tam giác CID có:
\(\widehat{EBI}=\widehat{DCI}\)
\(\widehat{BEI}=\widehat{CDI}\)
BE = CD
\(\Rightarrow\Delta BIE=\Delta CID\left(g-c-g\right)\)
d) Do \(\Delta BIE=\Delta CID\Rightarrow IB=IC\)
Lại có AB = AC nên IA là trung trực của BC
Vậy IA đi qua trung điểm F của BC hay A, I, F thẳng hàng.

Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath
a:AD+DB=AB
AE+EC=AC
mà AD=AE: AB=AC
nên DB=EC
b: Xet ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDBC=ΔECB
c: Xét ΔOCB có góc OCB=góc OBC
nên ΔOBC cân tại O