NC
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
26 tháng 4 2018
a) Ta có: ΔABC cân tại A
Nên: AB=AC
Mà: CN là đường trung tuyến => NB=NA
BM là đường trung tuyến => MA=MC
Suy ra: NB=NA=MA=MC
Xét ΔBNC và ΔCMB
Có: BN=CM (cmt)
\(\widehat{B}\)=\(\widehat{C}\)(do ΔABC cân)
BC chung
Suy ra: ΔBNC=ΔCMB (c-g-c)
14 tháng 5 2023
Xét ΔABM và ΔACN có
AB=AC
góc BAM chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
14 tháng 5 2023
Mình xin phép sửa đề:
Cho tam giác ABC cân tại A , các đường trung tuyến BM và CN cắt nhau tại G
Chứng minh tam giác ABN = tam giác ACN , từ đó suy ra BM=CN
`------`
\(\text{GT | AB = AC, }\widehat{\text{B}}=\widehat{\text{C}}\)
\(\text{CM | BM = CN}\)
\(\text{BM là đường trung tuyến}\)
`->`\(\text{MA = MC (1)}\)
\(\text{CN là đường trung tuyến}\)
`->`\(\text{NA = NB (2)}\)
`\Delta ABC` cân tại A
`->`\(\widehat{\text{B}}=\widehat{\text{C}}\text{, AB = AC (3)}\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
`->`\(\text{NA = NB = MA = MC}\)
Xét `\Delta ABM` và `\Delta ACN`:
\(\left\{{}\begin{matrix}\text{BM = CN}\\\widehat{\text{B}}=\widehat{\text{C}}\\\text{BC chung}\end{matrix}\right.\)
`=> \Delta ABM = \Delta ACN (c-g-c)`
`->`\(\text{BM = CN (2 cạnh tương ứng).}\)
22 tháng 5 2022
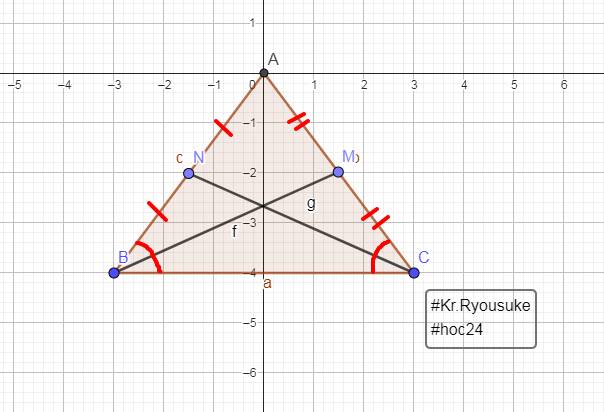
a: Xét ΔBNC và ΔCMB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó; ΔBNC=ΔCMB
b: Sửa đề: Cm ΔANM cân tại A
Xét ΔANM có AN=AM
nên ΔANM cân tại A
11 tháng 4 2023
Xét ΔABC có
BM,CN lần lượt là các đường trung tuyến
BM cắt CN tại I
=>I là trọng tâm
=>AI là đường trung tuyến của ΔACB
ΔABC cân tại A
mà AI là đường trung tuyến
nên AI vuông góc CB
=>AI là trung trực của BC
8 tháng 4 2016
a. Ta xét \(\Delta BCNvà\Delta CMB\)
có BC chung
góc B = góc C ( Hai góc ở đáy của tam giác cân)
BN = CM ( BN=\(\frac{1}{2}AB=\frac{1}{2}AC=CM\)
Suy ra tam giác BCN = tam giác CMB ( C-G-C)
b. Ta có tam giác BCN = tam giác CMB
suy ra góc BCN = góc CBM ( hai góc tương ứng)
tam giác BKC có góc KBC= góc KCB nên tam giác BKC cân tại K
c. Xét \(\Delta BKC\)
có BC< KB + KC ( BĐT tam giác) (1)
mà BK = 2.KM, CK = 2.KN mà BK= CK, KM =KN (2)
từ (1) và (2) suy ra BC < KB +KC =4.KM
Vậy BC < 4.KM
17 tháng 9 2023
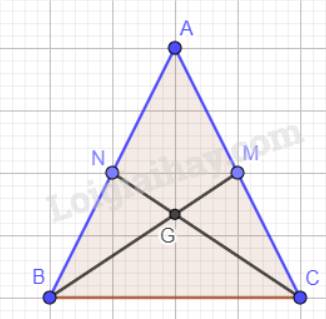
a) Tam giác ABC cân tại A nên AB = AC. M, N lần lượt là trung điểm của cạnh AC, AB nên AM = AN.
Xét tam giác ABM và tam giác ACN có: AM = AN; \(\widehat A\)chung; AB = AC.
Vậy \(\Delta ABM = \Delta ACN\)(c.g.c) hay BM = CN.
b) Xét tam giác ABC có G là giao điểm của hai đường trung tuyến BM và CN nên G là trọng tâm tam giác ABC. Do đó:
\(GB = \dfrac{2}{3}BM;GC = \dfrac{2}{3}CN\). Mà BM = CN nên GB = GC.
Vậy tam giác GBC cân tại G.
U
16 tháng 6 2020
C) MN // BC
o l m . v n
a, tam giác ABC cân tại A (gt)
=> AB = AC (Đn)
có M;N lần lượt là trung điểm của AC;AB (gt) => AM = MC = 1/2AC và AN = BN = 1/2BC (tc)
=> AN = AM = BN = CM
xét tam giác NBC và tam giác MCB có : BC chung
^ABC = ^ACB do tam giác ABC cân tại A (Gt)
=> tam giác NBC = tam giác MCB (c-g-c) (1)
b, (1) => ^KBC = ^KCB (đn)
=> tam giác KBC cân tại K (dh)
c, có tam giác ABC cân tại A (gt) => ^ABC = (180 - ^BAC) : 2 (tc)
có AM = AN (câu a) => tam giác AMN cân tại A (đn) => ^ANM = (180 - ^BAC) : 2 (tc)
=> ^ABC = ^ANM mà 2 góc này đồng vị
=> MN // BC (đl)
Lời giải:
$K$ là giao điểm của 2 đường trung tuyến $BM,CN$
$\Rightarrow K$ là trọng tâm tam giác $ABC$
$\Rightarrow KB=\frac{2}{3}BM$
$\Rightarrow 3KB=2BM$
$\Rightarrow 3KB=2(KB+KM)$
$\Rightarrow KB=2KM\Rightarrow KM=\frac{1}{2}KB$