
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


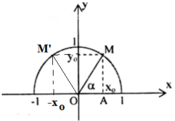
Gọi M(xo; yo) nằm trên nửa đường tròn đơn vị sao cho ∠xOM = α
Khi đó điểm M'(-xo; yo) trên nửa đường tròn đơn vị sao cho ∠xOM' = 180o - α (tức là ∠xOM' là bù với ∠xOM = α)
Do đó: sinα = yo = sin(180o - α)
cosα = xo = -(-xo) = -cos(180o - α)

Ta có:
\(\begin{array}{l}\cos {30^o} = \sin \left( {{{90}^o} - {{30}^o}} \right) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\sin {150^o} = \sin \left( {{{180}^o} - {{150}^o}} \right) = \sin {30^o} = \frac{1}{2};\\\tan {135^o} = - \tan \left( {{{180}^o} - {{135}^o}} \right) = - \tan {45^o} = - 1\end{array}\)
\( \Rightarrow E = 2.\frac{{\sqrt 3 }}{2} + \frac{1}{2} - 1 = \sqrt 3 - \frac{1}{2}.\)

Cho α và β là hai góc khác nhau và bù nhau. Ta có:
* sin α = sin β .
* cos α = − cos β .
* tan α = − tan β .
* cot α = − cot β .
Chọn D.

Ta có: Hai góc bù nhau có tổng số đo bằng 1800
Số đo góc xOy là: 1800 - 500= 1300
=> Góc xOy =1300
Ta có: Hai góc bù nhau có tổng số đo bằng 180° Số đo góc xOy là: 180° - 50°= 130°=> Góc xOy =130°

Chọn C.
Hai góc α và β bù nhau nên sinα = sinβ và cosα = - cosβ.
Do đó P = cosα.cosβ- sinα.sinβ.
= -cos2α – sin2α = -1

a) Đúng
Giải thích: Nhận thấy a→ = -3.i→
Vì –3 < 0 nên a→ và i→ ngược hướng.
b) Đúng.
Giải thích:
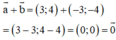
⇒ a→ = -b→ nên a→ và b→ là hai vec tơ đối nhau.
c) Sai
Giải thích:
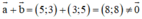
⇒ a→ ≠ -b→ nên a→ và b→ không phải là hai vec tơ đối nhau.
d) Đúng
Nhận xét SGK : Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.

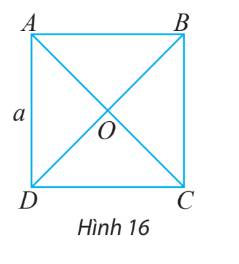
a) \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\) là:
\(\overrightarrow {AO} \)và \(\overrightarrow {OC} \); \(\overrightarrow {CO} \) và \(\overrightarrow {OA} \); \(\overrightarrow {DO} \) và \(\overrightarrow {OB} \); \(\overrightarrow {OD} \) và \(\overrightarrow {BO} \)
b) Trong hình chỉ có 2 đoạn thẳng AC và BD có độ dài là \(a\sqrt 2\).
Do đó hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\) là:
\(\overrightarrow {AC} \)và \(\overrightarrow {CA} \); \(\overrightarrow {BD} \) và \(\overrightarrow {DB} \).
Gọi M(x0;y0) là điểm M trên nửa đường tròn đơn vị sao cho góc xOM = α. Khi đó M’ trên nửa đường tròn đơn vị sao cho ∠xOM’ = 180° – a (tức là góc xOM’ là bù với góc xOM = a) có toạ độ M’ (-x0;y0)
Do đó: sina = y0 = sin(180° – a) cosa = x0 = -(-x0) = -sin(180° – a)