Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

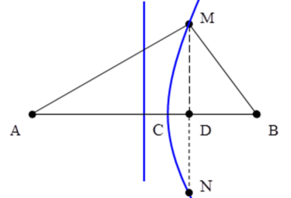
Số đường hyperbol cực đại cắt MN bằng số điểm cực đại trên CD
+Ta có AM – BM = AC – BC = 7cm
Và AC + BC = AB = 13cm suy ra AC = 10cm
+Ta lại có AM2 – AD+2 = BM2 – DB2
Và DB = AB – AD suy ra AD = 11,08cm
+Xét một điểm bất kì trên AB, điều kiện để điểm đó cực đại là :
\(d_2-d_1=k\lambda;d_2+d_1=AB\Rightarrow d_2=\frac{\left(AB+k\lambda\right)}{2}\)
+ số điểm cực đại trên AC là: \(0\le d_2\le AC\Leftrightarrow0\le\)\(\frac{AB+k\lambda}{2}\le AC\Leftrightarrow-\frac{AB}{\lambda}\le k\le\)\(\frac{2AC-AB}{\lambda}\)
\(\Leftrightarrow-10,8\le k\le5,8\Rightarrow\) có 16 điểm cực đại
+ số cực đại trên AD: \(0\le d_2\le AD\Leftrightarrow0\le\frac{AB+k\lambda}{2}\le AD\Leftrightarrow\)\(-\frac{AB}{\lambda}\le k\le\frac{2AD-AB}{\lambda}\)
\(\Leftrightarrow-10,8\le k\le7,6\Rightarrow\) có 18 điểm cực đại
Vậy trên CD có 18 – 16 = 2 cực đại, suy ra có 2 đường hyperbol cực đại cắt MN.
\(\rightarrow\) Chọn C



cực đại là:

Vậy trên CD có 18-16= 2 cực đại, suy ra có 2 đường hyperbol cực đại cắt MN
Đáp án C

Đáp án B
Ta có ![]() nên tam giác AMB vuông tại M.
nên tam giác AMB vuông tại M.
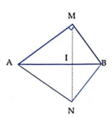
Mà ![]() suy ra IB= 9 cm.
suy ra IB= 9 cm.
Xét trên đoạn IM, số điểm dao động với biên độ cực đại là
![]() . Vậy trên đoạn IM có 1 điểm dao động với biên độ cực đại.
. Vậy trên đoạn IM có 1 điểm dao động với biên độ cực đại.
Do tính chất đối xứng IN cũng có một điểm dao động với biên độ cực đại.
Vậy trên MN có 2 điểm dao động vơi biên độ cực đại.

A,B là 2 nguồn cùng pha nên đường trung trực của AB dao động cực đại.
Giữa M và đường trung trực của AB có 3 dãy dực đại khác => M nằm trên dãy cực đại k = 4
\(d_2-d_1=(k+\frac{\triangle\varphi}{2\pi})\lambda = (4+0)\lambda \Rightarrow \lambda = \frac{d_2-d_1}{4}=\frac{21-19}{4}=0.5cm \Rightarrow v = f.\lambda = 80.0,5=40cm/s.\)

Đáp án C
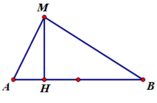
Dễ tìm chứng minh được tam giác MAB vuông tại M.
Có A H = M A 2 A B = 3 , 6 ( c m ) ; B H = M B 2 A B = 6 , 4 ( c m )
Số đường cực đại cắt qua MH là nghiệm k của bất pt:
A H − B H λ ≤ k ≤ A M − B M λ ⇔ − 0 , 93 ≤ k ≤ − 0 , 67 . Vì k nguyên nên bất pt này vô nghiệm. Vậy không có đường cực đại nào cắt MH.
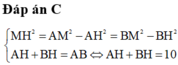
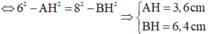

Chọn C