Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(1+1+1\right)!=6\)
\(2+2+2=6\)
\(\left(3+3-3\right)!=6\)
\(\sqrt{4}+\sqrt{4}+\sqrt{4}=6\)
\(5+5:5=6\)
\(7-7:7=6\)
\(\sqrt{8+\left(8:8\right)}!=6\)
\(\left(9-9\right)+\sqrt{9}!=6\)
\(\sqrt{10-\left(10:10\right)}!=6\)
Tất cả các phép đều sai
~~ tk mk nhé....~~
Ai tk mk mk tk lại ~~~
Kb lun nha....n_n

bạn ơi, đề nó cho +, -, x, : vs dấu ngoặc đơn chứ lm gì ai cho dấu / đâu mà bạn lm

Gọi x là tần số của điểm 4 (x > 0; x ∈ N)
Số học sinh của lớp:
2 + x + 10 + 12 + 7 + 6 + 4 + 1 = 42 + x
Vì điểm trung bình bằng 6,06 nên:
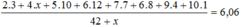
⇔ 6 + 4x + 50 + 72 + 49 + 48 + 36 + 10 = 6,06(42 + x)
⇔ 271 + 4x = 254,52 + 6,06x ⇔ 16,48 = 2,06x
⇔ x = 8 (thỏa mãn điều kiện đặt ra)
Vậy ta có kết quả điền vào như sau:
| Điểm (x) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Tần số (f) | 0 | 0 | 2 | 8 | 10 | 12 | 7 | 6 | 4 | 1 | N = 50 |

a) −x2+21−5x−x2+21−5x =x2+2−(1−5x)=x2+2−(1−5x) =x2+25x−1=x2+25x−1;
b) −4x+15−x−4x+15−x =4x+1−(5−x)=4x+1−(5−x) =4x+1x−5

\(M=\dfrac{3a-2b}{2a+5}+\dfrac{3b-a}{b-5}\)
\(=\dfrac{\left(3a-2b\right)\left(b-5\right)+\left(3b-a\right)\left(2a+5\right)}{\left(2a+5\right)\left(b-5\right)}\)
\(=\dfrac{3ab-15a-2b^2+10b+6ab+15b-2a^2-5a}{\left(2a+5\right)\left(b-5\right)}\)
\(=\dfrac{-2a^2-20a-2b^2+25b+9ab}{\left(2a+5\right)\left(b-5\right)}\)

Đặt (a + b)3 = a3 + 3a2b + 3ab2 + b3 = 8x3 + 12x2 + ... + ...
= (2x)3 + 3.(2x)2.1 + ... + ...
=> a = 2x ; b = 1 => 8x3 + 12x2 + 6x + 1 = (2x + 1)