
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Gọi biểu thức trên là A.
\(ĐK:x\ge0\). Ta có: \(A=\frac{\sqrt{x}-3}{\sqrt{x}+1}=\frac{\sqrt{x}}{\sqrt{x}+1}-\frac{3}{\sqrt{x}+1}\) (1)
Để \(x\in Z\) thì \(\frac{3}{\sqrt{x}+1}\in Z\Leftrightarrow\sqrt{x}+1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\sqrt{x}=\left\{0;-2;2;-4\right\}\) nhưng do không có căn bậc 2 của số âm nên:
\(\sqrt{x}\in\left\{0;2\right\}\Leftrightarrow x\in\left\{0;4\right\}\). Thay vào (1) để thử lại ta thấy chỉ có x = 0 thỏa mãn.
Vậy có 1 nghiệm là x = 0
b) Gọi biểu thức trên là B. ĐK: \(x\ge0\)
\(B=\frac{2\left(\sqrt{2}-5\right)}{\sqrt{x}+1}=\frac{2\sqrt{2}-10}{\sqrt{x}+1}=\frac{2\sqrt{2}}{\sqrt{x}+1}-\frac{10}{\sqrt{x}+1}\)
Để \(x\in Z\) thì \(\frac{10}{\sqrt{x}+1}\in Z\Leftrightarrow\sqrt{x}+1\inƯ\left(10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
Đến đây bạn tiếp tục lập bảng tìm \(\sqrt{x}\) rồi bình phương tất cả các giá trị của \(\sqrt{x}\) để tìm được các giá trị của x nhé!. Nhưng lưu ý rằng làm xong phải thử lại bằng cách thế vào B để tìm nghiệm chính xác nhất nhé!
c) Tương tự như trên,bạn tự làm
d) Tương tự như câu a),bạn tự làm. Mình lười òi =))

a: Sửa đề: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3+4⋮\sqrt{x}-3\)
=>\(4⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
=>\(x\in\left\{16;4;25;1;49\right\}\)
b: 
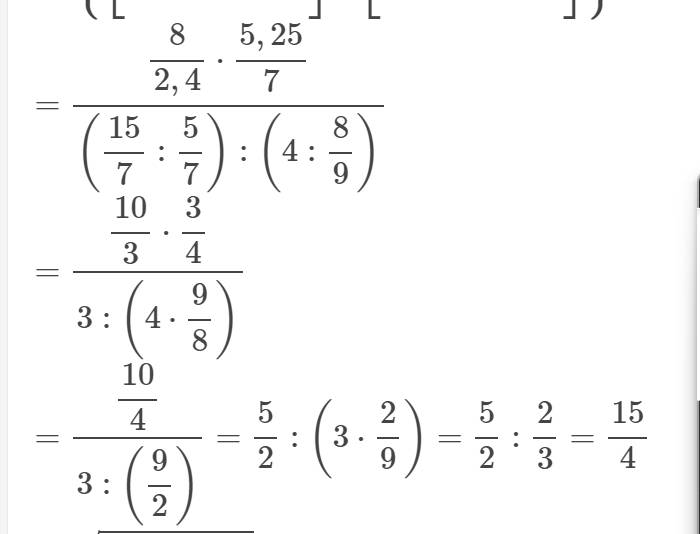

1) ĐKXĐ: \(x\ge0\)
\(\sqrt{x}=2\sqrt{2}\Rightarrow x=8\left(tmđkxđ\right)\)
2) ĐKXĐ: \(x\ge-1\)
\(\sqrt{\frac{x+1}{2}}=\frac{\sqrt{5}}{2}\)
\(\Leftrightarrow\frac{x+1}{2}=\frac{5}{4}\)
\(\Leftrightarrow2x+2=5\Leftrightarrow x=\frac{3}{2}\left(TMĐKXĐ\right)\)
1,
\(\sqrt{x}=2\sqrt{2}\)
=> \(\left(\sqrt{x}\right)=\left(2\sqrt{2}\right)^2\)
=> \(x=8\)
2.
\(\sqrt{\frac{x+1}{2}}=\frac{\sqrt{5}}{2}\)
=> \(\left(\sqrt{\frac{x+1}{2}}\right)=\left(\frac{\sqrt{5}}{2}\right)^2\)
=> \(\frac{x+1}{2}=\frac{5}{4}\)
=> 4 ( x + 1 ) = 5.2
=> 4x + 4 = 10
=> 4x = 6
=. x = \(\frac{3}{2}\)
\(\sqrt{x-1}=2\)
\(\Rightarrow x-1=4\)
\(\Rightarrow x=5\)
hok tốt
Ta có:
\(\sqrt{x-1}=2\)
\(\Leftrightarrow x-1=2^2\)
\(\Leftrightarrow x-1=4\)
\(\Leftrightarrow x=5\)
Vậy x=5