PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 8 2020
Căn bậc lẻ luôn luôn thỏa mãn, ko cần phải xét cứ thay thẳng giá trị thôi
11 tháng 7 2016
a) \(3\sqrt{a^2-4a+4}=3\sqrt{\left(a-2\right)^2}=3\left|a-2\right|=3\left(a-2\right)\) (vì \(a\ge2\))
b) \(2\sqrt{9a^2+12a+4}=2\sqrt{\left(3a+2\right)^2}=2\left|3a+2\right|=2\left(-3a-2\right)=-2\left(3a+2\right)\) (vì \(a< -\frac{2}{3}\))
NN
28 tháng 8 2020
\(ĐKXĐ:a\ge3\)
\(25\sqrt{\frac{a-3}{25}}-7\sqrt{\frac{4a-12}{9}}-7\sqrt{a^2-9}+18\sqrt{\frac{9a^2-81}{81}}=0\)
\(\Leftrightarrow25.\sqrt{\frac{1}{25}.\left(a-3\right)}-7\sqrt{\frac{4}{9}.\left(a-3\right)}-7\sqrt{a^2-9}+18\sqrt{\frac{9}{81}.\left(a^2-9\right)}=0\)
\(\Leftrightarrow25.\sqrt{\frac{1}{25}}.\sqrt{a-3}-7.\sqrt{\frac{4}{9}}.\sqrt{a-3}-7\sqrt{a^2-9}+18.\sqrt{\frac{9}{81}}.\sqrt{a^2-9}=0\)
\(\Leftrightarrow25.\frac{1}{5}.\sqrt{a-3}-7.\frac{2}{3}.\sqrt{a-3}-7\sqrt{a^2-9}+18.\frac{1}{3}.\sqrt{a^2-9}=0\)
\(\Leftrightarrow5\sqrt{a-3}-\frac{14}{3}.\sqrt{a-3}-7\sqrt{a^2-9}+6\sqrt{a^2-9}=0\)
\(\Leftrightarrow\frac{1}{3}.\sqrt{a-3}-\sqrt{a^2-9}=0\)
\(\Leftrightarrow\frac{1}{3}\sqrt{a-3}-\sqrt{\left(a-3\right)\left(a+3\right)}=0\)
\(\Leftrightarrow\sqrt{a-3}.\left(\frac{1}{3}-\sqrt{a+3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{a-3}=0\\\frac{1}{3}-\sqrt{a+3}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}a-3=0\\\sqrt{a+3}=\frac{1}{3}\end{cases}}\Leftrightarrow\orbr{\begin{cases}a=3\\a+3=\frac{1}{9}\end{cases}}\Leftrightarrow\orbr{\begin{cases}a=3\\a=\frac{-26}{9}\end{cases}}\)
mà \(a\ge3\)\(\Rightarrow a=\frac{-26}{9}\)không thỏa mãn
Vậy \(a=3\)
NC
28 tháng 8 2020
Bài làm:
đk: \(a\ge3\)
Ta có: \(25\sqrt{\frac{a-3}{25}}-7\sqrt{\frac{4a-12}{9}}-7\sqrt{a^2-9}+18\sqrt{\frac{9a^2-81}{81}}=0\)
\(\Leftrightarrow5\sqrt{a-3}+\frac{14}{3}\sqrt{a-3}-7\sqrt{a^2-9}+6\sqrt{a^2-9}=0\)
\(\Leftrightarrow\sqrt{a^2-9}=\sqrt{a-3}\)
\(\Leftrightarrow\left|a^2-9\right|=\left|a-3\right|\)
\(\Leftrightarrow\orbr{\begin{cases}a^2-9=a-3\\a^2-9=3-a\end{cases}}\Leftrightarrow\orbr{\begin{cases}a^2-a-6=0\\a^2+a-12=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}\left(a-3\right)\left(a+2\right)=0\\\left(a-3\right)\left(a+4\right)=0\end{cases}}\)
=> \(a\in\left\{-4;-2;3\right\}\)
Mà theo đk thì \(a\ge3\) => a = 3 (thỏa mãn)
Vậy a = 3
AT
17 tháng 8 2018
\(A=\left(x-2\right)\cdot\sqrt{\dfrac{9}{\left(x-2\right)^2}}+3=\dfrac{3\left(x-2\right)}{\left|x-2\right|}+3=\dfrac{3\left(x-2\right)}{-\left(x-2\right)}=-3+3=0\)
\(B=\sqrt{\dfrac{a}{6}}+\sqrt{\dfrac{2a}{3}}+\sqrt{\dfrac{3a}{2}}=\dfrac{\sqrt{a}}{\sqrt{6}}+\dfrac{\sqrt{2a}}{\sqrt{3}}+\dfrac{\sqrt{3a}}{\sqrt{2}}=\dfrac{\sqrt{a}+2\sqrt{a}+3\sqrt{a}}{\sqrt{6}}=\dfrac{6\sqrt{a}}{\sqrt{6}}=\sqrt{6a}\)
\(E=\sqrt{9a^2}+\sqrt{4a^2}+\sqrt{\left(1-a\right)^2}+\sqrt{16a^2}=3\left|a\right|+2\left|a\right|+\left|1-a\right|+4\left|a\right|=9\left|a\right|+1-a=-9a+1-a=-10a+1\)
\(F=\left|x-2\right|\cdot\dfrac{\sqrt{x^2}}{x}=\left|x-2\right|\cdot\dfrac{\left|x\right|}{x}=\dfrac{x\left(x-2\right)}{x}=x-2\)
\(H=\dfrac{x^2+2\sqrt{3}\cdot x+3}{x^2-3}=\dfrac{\left(x+\sqrt{3}\right)^2}{\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)}=\dfrac{x+\sqrt{3}}{x-\sqrt{3}}\)
\(I=\left|x-\sqrt{\left(x-1\right)^2}\right|-2x=\left|x-\left(-\left(x-1\right)\right)\right|-2x=\left|x+x-1\right|-2x=\left|2x-1\right|-2x=1-4x\)
5 tháng 8 2019
1.
a) \(A=\sqrt{1}-4a+4a^2-2a\)
\(A=4a^2-6a+1\)
b) \(B=\frac{5-x}{x^2-10x+25}=\frac{-\left(x-5\right)}{\left(x-5\right)^2}=\frac{-1}{x-5}\)
c) \(C=\sqrt{\left(x-1\right)^2}+\frac{x-1}{\sqrt{x^2-2x+1}}\)
\(C=\left|x-1\right|+\frac{x-1}{\sqrt{\left(x-1\right)^2}}=\left|x-1\right|+\frac{x-1}{\left|x-1\right|}\)
+) Xét \(x-1>0\Leftrightarrow x>1\)ta có \(C=x-1+\frac{x-1}{x-1}=x-1+1=x\)
+) Xét \(x-1< 0\Leftrightarrow x< 1\)ta có \(C=1-x+\frac{x-1}{1-x}=1-x-1=-x\)
2.
a) \(\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{3}}\)
\(=\sqrt{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=\sqrt{4-3}=1\)
b) \(\sqrt{3\sqrt{2}-2\sqrt{3}}\cdot\sqrt{3\sqrt{2}+2\sqrt{3}}\)
\(=\sqrt{\left(3\sqrt{2}-2\sqrt{3}\right)\left(3\sqrt{2}+2\sqrt{3}\right)}\)
\(=\sqrt{\left(3\sqrt{2}\right)^2-\left(2\sqrt{3}\right)^2}\)
\(=\sqrt{18-12}=\sqrt{6}\)
c) Sửa luôn đề \(\sqrt{13-4\sqrt{3}}+\sqrt{7+4\sqrt{3}}\)
\(=\sqrt{\left(2\sqrt{3}\right)^2-2\cdot2\sqrt{3}\cdot1+1}+\sqrt{2^2+2\cdot2\cdot\sqrt{3}+3}\)
\(=\sqrt{\left(2\sqrt{3}-1\right)^2}+\sqrt{\left(2+\sqrt{3}\right)^2}\)
\(=\left|2\sqrt{3}-1\right|+\left|2+\sqrt{3}\right|\)
\(=2\sqrt{3}-1+2+\sqrt{3}\)
\(=3\sqrt{3}+1\)
23 tháng 8 2021
a, ĐK :a >= 3
\(25\sqrt{\frac{a-3}{25}}-7\sqrt{\frac{4a-12}{9}}-7\sqrt{a^2-9}+18\sqrt{\frac{9a^2-81}{81}}=0\)
\(\Leftrightarrow5\sqrt{a-3}-\frac{14}{3}\sqrt{a-3}-7\sqrt{\left(a-3\right)\left(a+3\right)}+6\sqrt{\left(a-3\right)\left(a+3\right)}=0\)
\(\Leftrightarrow\sqrt{a-3}\left(5-\frac{14}{3}-\sqrt{a+3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{a-3}=0\\\sqrt{a+3}=\frac{1}{3}\end{cases}}\Leftrightarrow\orbr{\begin{cases}a=3\left(tm\right)\\a=-\frac{2}{9}\left(loai\right)\end{cases}}\)
b, \(ĐK:x\ge-\frac{1}{2}\)
\(\Leftrightarrow3\sqrt{2x+1}-2\sqrt{2x+1}+\frac{1}{3}\sqrt{2x+1}=4\)
\(\Leftrightarrow\frac{4}{3}\sqrt{2x+1}=4\)
\(\Leftrightarrow\sqrt{2x+1}=3\)
\(\Leftrightarrow x=4\left(tm\right)\)
23 tháng 8 2021
a) đk: \(a\ge3\)
pt \(\Leftrightarrow25\frac{\sqrt{a-3}}{\sqrt{25}}-7\frac{\sqrt{4\left(a-3\right)}}{\sqrt{9}}-7\sqrt{a^2-9}+18\frac{\sqrt{9\left(a^2-9\right)}}{\sqrt{81}}=0\)
\(\Leftrightarrow5\sqrt{a-3}-\frac{7.2}{3}\sqrt{a-3}-7\sqrt{a^2-9}+\frac{18.3}{9}\sqrt{a^2-9}=0\)
\(\Leftrightarrow5\sqrt{a-3}-\frac{14}{3}\sqrt{a-3}-7\sqrt{a^2-9}+6\sqrt{a^2-9}=0\)
\(\Leftrightarrow\frac{1}{3}\sqrt{a-3}-\sqrt{a^2-9}=0\)
\(\Leftrightarrow\frac{1}{3}\sqrt{a-3}=\sqrt{a^2-9}\)
\(\Leftrightarrow\frac{1}{9}\left(a-3\right)=a^2-9\)
\(\Leftrightarrow a^2-\frac{1}{9}a-\frac{26}{3}=0\Leftrightarrow\orbr{\begin{cases}a=3\left(tm\right)\\a=-\frac{26}{9}\left(loại\right)\end{cases}}\)
15 tháng 7 2017
a) \(\sqrt{-9a}-\sqrt{9+12a+4a^2}\) \(=\sqrt{9.\left(-a\right)}-\sqrt{\left(3+2a\right)^2}=3\sqrt{-a}-\left|3+2a\right|\)
\(=3\sqrt{9}-\left|3+2\left(-9\right)\right|=3.3-15=-6\)
b) \(1+\dfrac{3m}{m-2}\sqrt{m^2-4x+4}=1+\dfrac{3m}{m-2}\sqrt{\left(m-2\right)^2}=1+\dfrac{3m\left|m-2\right|}{m-2}\)
\(=\left\{{}\begin{matrix}1+3m\left(nếu\left(m-2\right)>0\right)\\1-3m\left(nến\left(m-2\right)< 0\right)\end{matrix}\right.\) \(=\left\{{}\begin{matrix}1+3m\left(nếu\left(m>2\right)\right)\\1-3m\left(nếu\left(m< 2\right)\right)\end{matrix}\right.\)
ta có : \(m=1,5< 2\) vậy giá trị của biểu thức tại m = 1,5 là \(1-3m\) = \(1-3.1,5=-3,5\)
c) \(\sqrt{1-10a+25a^2}-4a=\sqrt{\left(1-5a\right)^2}-4a=\left|1-5a\right|-4a\)
\(=\left\{{}\begin{matrix}1-9a\left(nếu\left(1-5a\right)\ge0\right)\\a-1\left(nếu\left(1-5a\right)< 0\right)\end{matrix}\right.\) \(=\left\{{}\begin{matrix}1-9a\left(nếu\left(a\le\dfrac{1}{5}\right)\right)\\a-1\left(nếu\left(a>\dfrac{1}{5}\right)\right)\end{matrix}\right.\)
ta có : \(a=\sqrt{2}>\dfrac{1}{5}\) vậy giá trị của biểu thức tại \(a=\sqrt{2}\) là a - 1 = \(\sqrt{2}-1\)
d) \(4x-\sqrt{9x^2+6x+1}=4x-\sqrt{\left(3x+1\right)^2}=4x-\left|3x+1\right|\)
\(=\left\{{}\begin{matrix}x-1\left(nếu\left(x\ge-\dfrac{1}{3}\right)\right)\\7x+1\left(nếu\left(x< -\dfrac{1}{3}\right)\right)\end{matrix}\right.\)
ta có : \(x=-\sqrt{3}< -\dfrac{1}{3}\) vậy giá trị của biểu thức tại \(x=-\sqrt{3}\) là \(7.\left(-\sqrt{3}\right)+1=1-7\sqrt{3}\)
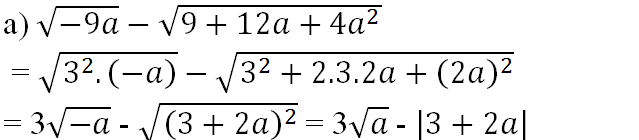
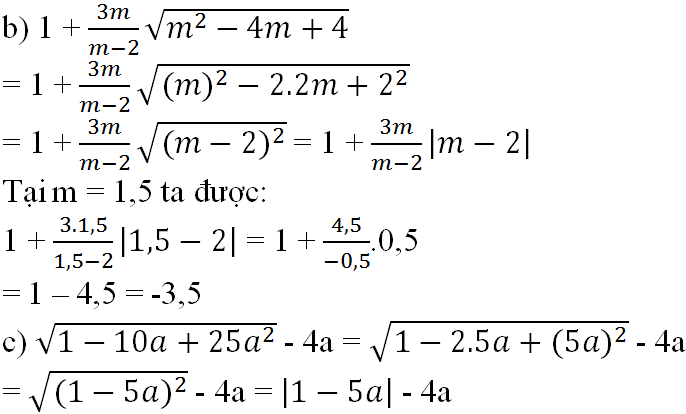
TL:
\(\sqrt{9a}+3\sqrt{4a}\)
\(=3\sqrt{a}+3.2\sqrt{a}\)
\(=3\sqrt{a}+6\sqrt{a}\)
\(=9\sqrt{a}\)
-HT-