

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn ra 1 chẵn trong 5 chẵn và 1 lẻ trong 5 lẻ có số cách chọn bằng
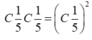
Chọn đáp án C.

a) \(\frac{7}{11}-\left(\frac{3}{5}+\frac{7}{11}\right)=-\frac{3}{5}\)
b) \(\left(\frac{11}{22}+\frac{5}{11}\right)-\frac{19}{22}=\frac{1}{11}\)
c) \(\frac{2}{9}.\frac{4}{5}+\frac{2}{9}.\frac{14}{5}=\frac{4}{5}\)
d) \(-\frac{3}{2}.\frac{7}{10}-\frac{3}{2}.\frac{1}{10}=-\frac{6}{5}\)
e) \(\left(0,75-1+\frac{1}{4}\right):\left(\frac{1515}{1616}+\frac{1616}{1717}\right)=0\)

Với mỗi cách chọn ra đúng 3 phần tử của tập A ta được một tập con gồm đúng 3 phần tử, nên số tập con cần tìm bằng C 10 3 .
Chọn đáp án C.

a) -2x+14=0
<=>-2x= - 14
<=>x = 7
Vậy phương trình có tập nghiệm x={7}
b)(4x-10) (x+5)=0
<=>4x-10=0 <=>4x=10 <=>x=5/2
<=>x+5=0 <=>x=-5
Vậy phương trình có tập nghiệm x={5/2;- 5}
c)\(\frac{1-x}{x+1}\) + 3=\(\frac{2x+3}{x+1}\)
ĐKXD: x+1 #0<=>x#-1(# là khác)
\(\frac{1-x}{x+1}\)+3=\(\frac{2x+3}{x+1}\)
<=>\(\frac{1-x}{x+1}\)+\(\frac{3.\left(x+1\right)}{x+1}\)=\(\frac{2x+3}{x+1}\)
<=>\(\frac{1-x}{x+1}\)+\(\frac{3x+3}{x+1}\)=\(\frac{2x+3}{x+1}\)
=>1-x+3x+3=2x+3
<=>-x+3x-2x=-1-3+3
<=>0x = -1 (vô nghiệm)
Vâyj phương trình vô nghiệm
d) 1,2-(x-0,8)=-2(0,9+x)
<=> 1,2-x+0,8=-1,8-2x
<=>-x+2x=-1,2-0,8-1,8
<=>x=-4
Vậy phương trình có tập nghiệm x={-4}