Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Ta có: \(\dfrac{3}{-4}=\dfrac{-3}{4};\dfrac{-12}{15}=\dfrac{-4}{5};\dfrac{-15}{20}=\dfrac{-3}{4};\dfrac{24}{-32}=\dfrac{-3}{4};\dfrac{-20}{28}=\dfrac{-5}{7};\dfrac{-27}{36}=\dfrac{-3}{4}\)
Vậy trong các phân số trên những phân số biểu diễn số hữu tỉ \(\dfrac{3}{-4}\) là:
\(\dfrac{3}{-4}=\dfrac{-15}{20}=\dfrac{24}{-32}=\dfrac{-27}{36}\)
2.
a. Ta có: \(x=\dfrac{2}{-7}=\dfrac{-2}{7}=\dfrac{-22}{77};y=\dfrac{-3}{11}=\dfrac{-21}{77}\)
Vì \(-22< -21\) nên \(\dfrac{2}{-7}< \dfrac{-3}{11}\)
Vậy x < y
b. Ta có: \(x=\dfrac{-213}{300};y=\dfrac{18}{-25}=\dfrac{-18}{25}=\dfrac{-216}{300}\)
Vì \(-213>-216\) nên \(\dfrac{-213}{300}>\dfrac{18}{-25}\)
Vậy x > y
c. Ta có: \(x=-0,75=\dfrac{-3}{4};y=\dfrac{-3}{4}\)
Vì -3 = -3 nên \(-0,75=\dfrac{-3}{4}\)
Vậy x = y
3.
a.* Với a, b cùng dấu thì \(\dfrac{a}{b}>0\)
* Với a, b khác dấu thì \(\dfrac{a}{b}< 0\)
• Tổng quát: Số hữu tỉ \(\dfrac{a}{b}\left(a,b\in Z;b\ne0\right)\) dương nếu a,b cùng dấu; âm nếu a,b khác dấu; bằng 0 nếu a=0

bài 1) ta có : \(\dfrac{2x-y}{x+y}=\dfrac{2}{3}\Leftrightarrow2\left(x+y\right)=3\left(2x-y\right)\)
\(\Leftrightarrow2x+2y=6x-3y\Leftrightarrow4x=5y\Leftrightarrow\dfrac{x}{y}=\dfrac{5}{4}\)
vậy \(\dfrac{x}{y}=\dfrac{5}{4}\)
bài 1
\(\dfrac{2x-y}{x+y}=\dfrac{2}{3}\Leftrightarrow\dfrac{2.\dfrac{x}{y}-1}{\dfrac{x}{y}+1}=\dfrac{2.\dfrac{x}{y}+2-3}{\dfrac{x}{y}+1}=2-\dfrac{3}{\dfrac{x}{y}+1}=\dfrac{2}{3}\)
\(2-\dfrac{2}{3}=\dfrac{4}{3}=\dfrac{3}{\dfrac{x}{y}+1}\)
\(\left(\dfrac{x}{y}+1\right)=\dfrac{9}{4}\Rightarrow\dfrac{x}{y}=\dfrac{9}{4}-\dfrac{4}{4}=\dfrac{5}{4}\)

b: 2x^3-1=15
=>2x^3=16
=>x=2
\(\dfrac{x+16}{9}=\dfrac{y-25}{16}=\dfrac{z+9}{25}\)
=>\(\dfrac{y-25}{16}=\dfrac{z+9}{25}=\dfrac{18}{9}=2\)
=>y-25=32; z+9=50
=>y=57; z=41
d: 3/5x=2/3y
=>9x=10y
=>x/10=y/9=k
=>x=10k; y=9k
x^2-y^2=38
=>100k^2-81k^2=38
=>19k^2=38
=>k^2=2
TH1: k=căn 2
=>\(x=10\sqrt{2};y=9\sqrt{2}\)
TH2: k=-căn 2
=>\(x=-10\sqrt{2};y=-9\sqrt{2}\)

\(a,Đặt\dfrac{x}{y}=\dfrac{2}{3}\Leftrightarrow\dfrac{x}{2}=\dfrac{y}{3}=k\Leftrightarrow\left\{{}\begin{matrix}x=2k\\y=3k\end{matrix}\right.\\ A=\dfrac{2x-3y}{x-5y}=\dfrac{2\cdot2k-3\cdot3k}{2k-5\cdot3k}\\ =\dfrac{4k-9k}{2k-15k} \\ =\dfrac{5k}{13k}\\ =\dfrac{5}{13}\)
\(b,Thayx-y=7vàoB,tacó:\\ B=\dfrac{2x+7}{3x-y}+\dfrac{2y-7}{3y-x}\\ =\dfrac{2x+x-y}{3x-y}+\dfrac{2y-x+y}{3y-x}\\ =\dfrac{3x-y}{3x-y}+\dfrac{3y-x}{3y-x}\\ =1+1\\ =2\)
\(c,Đặt\dfrac{x}{3}=\dfrac{y}{5}=k\Leftrightarrow\left\{{}\begin{matrix}x=3k\\y=5k\end{matrix}\right.\\ C=\dfrac{5x^2+3y^2}{10x^2-3y^2}\\ =\dfrac{5\left(3k\right)^2+3\left(5k\right)^2}{10\left(3k\right)^2-3\left(5k\right)^2}\\ =\dfrac{45k^2+75k^2}{90k^2-75k^2}\\ =\dfrac{120k^2}{15k^2}\\ =8\)
\(d,\dfrac{a}{b}=\dfrac{5}{7}\Leftrightarrow\dfrac{a}{5}=\dfrac{b}{7}=k\Leftrightarrow\left\{{}\begin{matrix}a=5k\\b=7k\end{matrix}\right.\\ D=\dfrac{5a-b}{3a-2b}\\ =\dfrac{5\cdot5k-7k}{3\cdot5k-2\cdot7k}\\ =\dfrac{25k-7k}{15k-14k}\\ =\dfrac{18k}{k}=18\)
\(e,Thayx-y=5vàoE,tacó:\\ E=\dfrac{3x-5}{2x+y}-\dfrac{4y+5}{x+3y}\\ =\dfrac{3x-x+y}{2x+y}-\dfrac{4y+x-y}{x+3y}\\ =\dfrac{2x+y}{2x+y}-\dfrac{3y+x}{x+3y}\\ =1-1=0\)

a) Với x = 2/-7 = -2/7 và y = -3/11
Ta quy đồng mẫu số : x = -2/7 = -22/77 và y = -3/11 = -21/77
Ta có : -22 < -21. Do đó : x < y
b) Với x = -213/300 và y= 18/-25 = -18/25 = -216/300
Ta có : -216 < -213. Do đó : y < x
c) Với x = -0,75 và y = -3/4 = -0,75
Ta có : -0,75 = -0,75. Do đó : x = y

Câu 2:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{6}=\dfrac{x-y+z}{2-4+6}=\dfrac{8}{8}=1\)
Do đó: x=2; y=4; z=6

Bài1:
Ta có:
a)\(\sqrt{\dfrac{3^2}{5^2}}=\sqrt{\dfrac{9}{25}}=\dfrac{3}{5}\)
b)\(\dfrac{\sqrt{3^2}+\sqrt{42^2}}{\sqrt{5^2}+\sqrt{70^2}}=\dfrac{\sqrt{9}+\sqrt{1764}}{\sqrt{25}+\sqrt{4900}}=\dfrac{3+42}{5+70}=\dfrac{45}{75}=\dfrac{3}{5}\)
c)\(\dfrac{\sqrt{3^2}-\sqrt{8^2}}{\sqrt{5^2}-\sqrt{8^2}}=\dfrac{\sqrt{9}-\sqrt{64}}{\sqrt{25}-\sqrt{64}}=\dfrac{3-8}{5-8}=\dfrac{-5}{-3}=\dfrac{5}{3}\)
Từ đó, suy ra: \(\dfrac{3}{5}=\sqrt{\dfrac{3^2}{5^2}}=\dfrac{\sqrt{3^2}+\sqrt{42^2}}{\sqrt{5^2}+\sqrt{70^2}}\)
Bài 2:
Không có đề bài à bạn?
Bài 3:
a)\(\sqrt{x}-1=4\)
\(\Rightarrow\sqrt{x}=5\)
\(\Rightarrow x=\sqrt{25}\)
\(\Rightarrow x=5\)
b)Vd:\(\sqrt{x^4}=\sqrt{x.x.x.x}=x^2\Rightarrow\sqrt{x^4}=x^2\)
Từ Vd suy ra:\(\sqrt{\left(x-1\right)^4}=16\)
\(\Rightarrow\left(x-1\right)^2=16\)
\(\Rightarrow\left(x-1\right)^2=4^2\)
\(\Rightarrow x-1=4\)
\(\Rightarrow x=5\)

a. Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{2x}{5}=\dfrac{y}{7}=\dfrac{y-2x}{7-5}=\dfrac{24}{2}=12\)
\(\Rightarrow2x=12\cdot5=60\Rightarrow x=60:2=30\)
\(y=12\cdot7=84\)
Vậy x = 30 ; y = 84
b. Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+3y}{3+2\cdot3}=\dfrac{18}{9}=2\)
\(\Rightarrow x=2\cdot3=6\)
\(y=2\cdot2=4\)
Vậy x = 6 ; y = 4
c. Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{18}{9}=2\)
\(\Rightarrow x=2\cdot2=4\)
\(y=3\cdot2=6\)
\(z=4\cdot2=8\)
Vậy x = 4 ; y = 6 ; z = 8
d. Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x-y-z}{2-3-4}=\dfrac{15}{-5}=-3\)
\(\Rightarrow x=-3\cdot2=-6\)
\(y=-3\cdot3=-9\)
\(z=-3\cdot4=-12\)
Vậy \(x=-4;y=-6;z=-8\)

So sánh các số hữu tỉ:
a) và
và 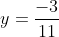
b)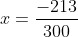 và
và 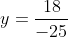
c) x = -0,75 và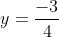
Lời giải:
a)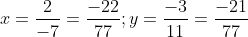
Vì -22 < -21 và 77> 0 nên x <y
b)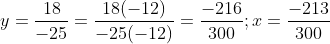
Vì -216 < -213 và 300 > 0 nên y < x
c)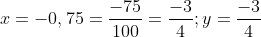
Vậy x=y
Lời giải:
a)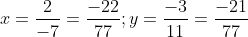
Vì -22 < -21 và 77> 0 nên x <y
b)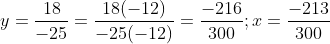
Vì -216 < -213 và 300 > 0 nên y < x
c)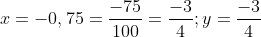
Vậy x=y