Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=2023\times2024\\ =\left(2022+1\right)\times2024\\ =2022\times2024+2024\\ B=2022\times2025\\ =2022\times\left(2024+1\right)\\ =2022\times2024+2022\)
Vì 2022 x 2024 = 2022 x 2024
=> 2024 > 2022
=> A> B
Cách 2
A= 2023 x 2024 = 4094552
B = 2022 x 2025 =4094550
Vì 4094552 > 4094550 = > A> B


a: \(B=\dfrac{154}{155+156}+\dfrac{155}{155+156}\)
\(\dfrac{154}{155}>\dfrac{154}{155+156}\)
\(\dfrac{155}{156}>\dfrac{155}{155+156}\)
=>154/155+155/156>(154+155)/(155+156)
=>A>B
b: \(C=\dfrac{2021+2022+2023}{2022+2023+2024}=\dfrac{2021}{6069}+\dfrac{2022}{6069}+\dfrac{2023}{6069}\)
2021/2022>2021/6069
2022/2023>2022/2069
2023/2024>2023/6069
=>D>C

\(A=\dfrac{2024^{2023}+1}{2024^{2024}+1}\)
\(2024A=\dfrac{2024^{2024}+2024}{2024^{2024}+1}=\dfrac{\left(2024^{2024}+1\right)+2023}{2024^{2024}+1}=\dfrac{2024^{2024}+1}{2024^{2024}+1}+\dfrac{2023}{2024^{2024}+1}=1+\dfrac{2023}{2024^{2024}+1}\)
\(B=\dfrac{2024^{2022}+1}{2024^{2023}+1}\)
\(2024B=\dfrac{2024^{2023}+2024}{2024^{2023}+1}=\dfrac{\left(2024^{2023}+1\right)+2023}{2024^{2023}+1}=\dfrac{2024^{2023}+1}{2024^{2023}+1}+\dfrac{2023}{2024^{2023}+1}=1+\dfrac{2023}{2024^{2023}+1}\)
Vì \(2024>2023=>2024^{2024}>2024^{2023}\)
\(=>2024^{2024}+1>2024^{2023}+1\)
\(=>\dfrac{2023}{2024^{2023}+1}>\dfrac{2023}{2024^{2024}+1}\)
\(=>A< B\)
\(#PaooNqoccc\)

\(C=\dfrac{2^{2024}-3}{2^{2023}-1}=\dfrac{2.2^{2023}-2-1}{2^{2023}-1}=\dfrac{2\left(2^{2023}-1\right)-1}{2^{2023}-1}=2-\dfrac{1}{2^{2023}-1}\)
\(D=\dfrac{2^{2023}-3}{2^{2022}-1}=\dfrac{2.2^{2022}-2-1}{2^{2022}-1}=\dfrac{2\left(2^{2022}-1\right)-1}{2^{2022}-1}=2-\dfrac{1}{2^{2022}-1}\)
Ta có
\(2^{2023}>2^{2022}\Rightarrow2^{2023}-1>2^{2022}-1\)
\(\Rightarrow\dfrac{1}{2^{2023}-1}< \dfrac{1}{2^{2022}-1}\Rightarrow2-\dfrac{1}{2^{2023}-1}>2-\dfrac{1}{2^{2022}-1}\)
\(\Rightarrow C>D\)

1. Giải:
Do \(5x+13B\in\left(2x+1\right)\Rightarrow5x+13⋮2x+1.\)
\(\Rightarrow2\left(5x+13\right)⋮2x+1\Rightarrow10x+26⋮2x+1.\)
\(\Rightarrow5\left(2x+1\right)+21⋮2x+1.\)
Do 5(2x+1)⋮2x+1⇒ Ta cần 21⋮2x+1.
⇒ 2x+1 ϵ B(21)=\(\left\{1;3;7;21\right\}.\)
Ta có bảng:
| 2x+1 | 1 | 3 | 7 | 21 |
| x | 0 | 1 | 3 | 10 |
| TM | TM | TM | TM |
Vậy xϵ\(\left\{0;1;3;10\right\}.\)
2. Giải:
Do (2x-18).(3x+12)=0.
⇒ 2x-18=0 hoặc 3x+12=0.
⇒ 2x =18 3x =-12.
⇒ x =9 x =-4.
Vậy xϵ\(\left\{-4;9\right\}.\)
3. S= 1-2-3+4+5-6-7+8+...+2021-2022-2023+2024+2025.
S= (1-2-3+4)+(5-6-7+8)+...+(2021-2022-2023+2024)+2025 Có 506 cặp.
S= 0 + 0 + ... + 0 + 2025.
⇒S= 2025.

\(A=\dfrac{10^{2024}+1}{10^{2023}+1}=\dfrac{10\left(10^{2023}+1\right)}{10^{2023}+1}-\dfrac{9}{10^{2023}+1}=1-\dfrac{9}{10^{2023}+1}\)
\(B=\dfrac{10^{2023}+1}{10^{2022}+1}=\dfrac{10\left(10^{2022}+1\right)}{10^{2022}+1}-\dfrac{9}{10^{2022}+1}=1-\dfrac{9}{10^{2022}+1}\)
Vì \(\dfrac{9}{10^{2023}+1}< \dfrac{9}{10^{2022}+1}\)
\(\Rightarrow A>B\)
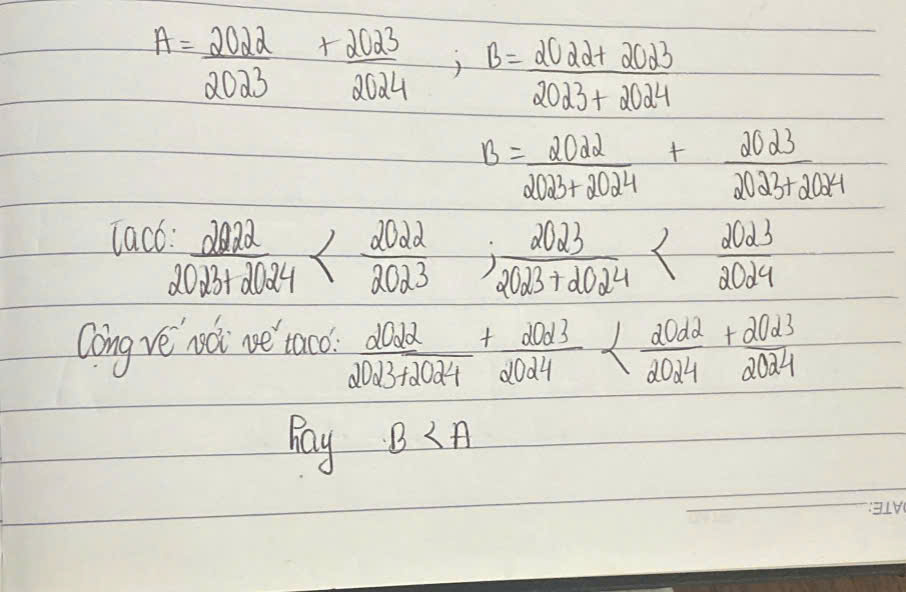




a) \(\dfrac{3}{7}>\dfrac{2}{7}>\dfrac{2}{8}=\dfrac{1}{4}>\dfrac{1}{9}\)
b) \(-\dfrac{5}{16}< 0< \dfrac{3}{4}\)
c) \(\dfrac{2024}{2023}>1>\dfrac{2022}{2025}\)
-------------------------
- Cả 3 câu mình đều dùng so sánh qua trung gian nhé, nghĩa là bạn lấy một số / phân số làm trung gian, nó bé hơn số này và lớn hơn số còn lại và nhiệm vụ là phải chứng minh được như thế
Lưu ý: Phân số cùng từ thì phân số nào có mẫu bé hơn thì nó lớn hơn và ngược lại. Phân số cùng mẫu thì tử nào bé hơn thì phân số đó bé hơn và ngược lại
cảm ơn