BH
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
5
VH
8
9 tháng 6 2021
\(S_{xq}=2\pi R.h=2\pi.5.7=70\pi\left(cm^2\right)\)
\(\Rightarrow B\)
-Chúc bạn học tốt-
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 12 2018
\(y'=\left(m^2-2\right)cosx-\dfrac{1}{cos^2x}\)
Để hàm số nghịch biến trên \(\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\Rightarrow y'\le0\) \(\forall x\in\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\)
Đặt \(cosx=t\Rightarrow0< t\le1\) \(\forall x\in\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\)
\(y'=\left(m^2-2\right)t-\dfrac{1}{t^2}\le0\) \(\Leftrightarrow m^2-2\le\dfrac{1}{t^3}\Leftrightarrow m^2\le\dfrac{1}{t^3}+2\) \(\forall t\in\text{(0;1]}\)
Đặt \(f\left(t\right)=\dfrac{1}{t^3}+2\Rightarrow m^2\le\min\limits_{\text{(0;1]}}f\left(t\right)\)
\(f'\left(t\right)=-\dfrac{3}{t^4}< 0\) \(\forall t\in\text{(0;1]}\) \(\Rightarrow f\left(t\right)\) nghịch biến \(\Rightarrow\min\limits_{\text{(0;1]}}f\left(t\right)=f\left(1\right)=3\)
\(\Rightarrow m^2\le3\Rightarrow-\sqrt{3}\le m\le\sqrt{3}\) \(\Rightarrow m=\left\{-1;0;1\right\}\)
\(\Rightarrow\) có 3 giá trị nguyên của m để hàm số nghịch biến trên \(\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\)
VN
1 tháng 6 2019
1. cô lập m: m>= -\(e^{\frac{\pi}{2}}\)+\(\sqrt[4]{e^{2x+1}}\)
2 bất phương trình có nghiệm vs mọi x=> m> max của vế phải
3 tìm max vế phải
CM
28 tháng 8 2017
Chọn A
Phương pháp:
Gọi giá tua là x (triệu đồng).
Lập hàm số tổng doanh thu theo x.
Xét hàm tìm GTLN của hàm số trên và kết luận.
Cách giải:
Gọi x (triệu đồng) là giá tua.
Số tiền được giảm đi so với ban đầu là 2-x.
Số người tham gia được tăng thêm nếu bán với giá x là: 
Số người sẽ tham gia nếu bán giá x là: 150 + (400-200x) = 550 - 220x
Tổng doanh thu là: f(x) = x(550-220x) 
Bảng biến thiên
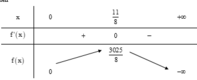
Dựa vào bảng biến thiên ta thấy f(x) đạt giá trị lớn nhất khi 
Vậy công ty cần đặt gói tua 1375000 đồng thì tổng doanh thu sẽ cao nhất là 378125000 đồng.
3,14XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
Số pi là số đặc trưng của hình tròn
Nó dùng để tính chu vi và có giá trị gần đúng là 3,14