Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án D.
Có y ' = 3 x 2 + 6 m - 16 x + 3 m 2 - 16 m
Có y ' = 0
suy ra hàm số đã cho nghịch biến trên - m ; 16 3 - m
Do đó y c d b
Khi đó y' là hàm số bậc ba. Phương trình y'=0 có ít nhất một nghiệm đơn hoặc bội lẻ và đổi dấu qua nghiệm đó. Do đó mệnh đề (*) sai. Suy ra loại m 2 - 3 m + 2 ≠ 0
Chọn A
3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)
Đáp án B
Đặt 
.
Vớ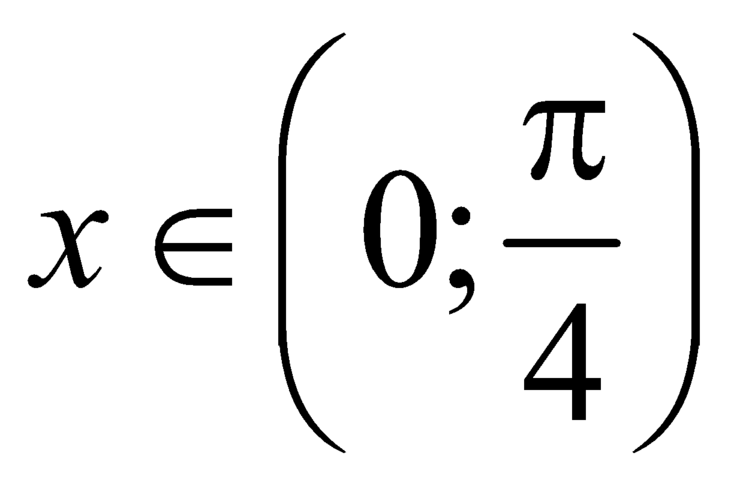i 
thì 
, hàm số trở thành 
.
Đạo hàm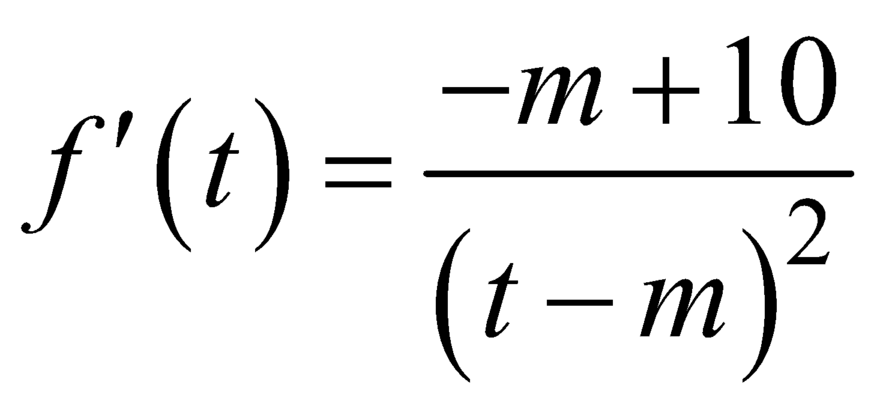 
.
Hàm số đồng biến trên 
khi
.
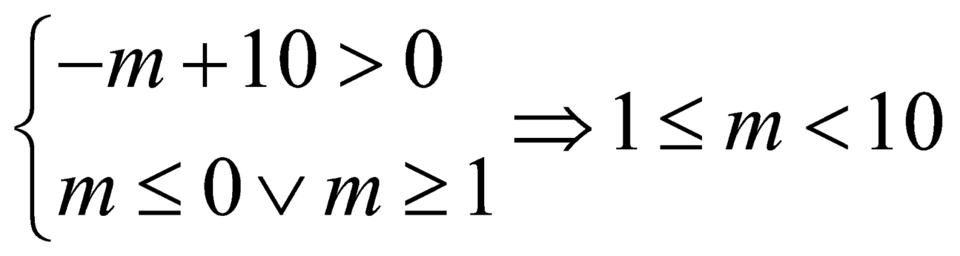Vậy có 9 giá trị nguyên của m
khi 
y = x – sinx, x ∈ [0; 2 π ].
y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2 π ]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2 π .
Vậy hàm số đồng biến trên đoạn [0; 2 π ].
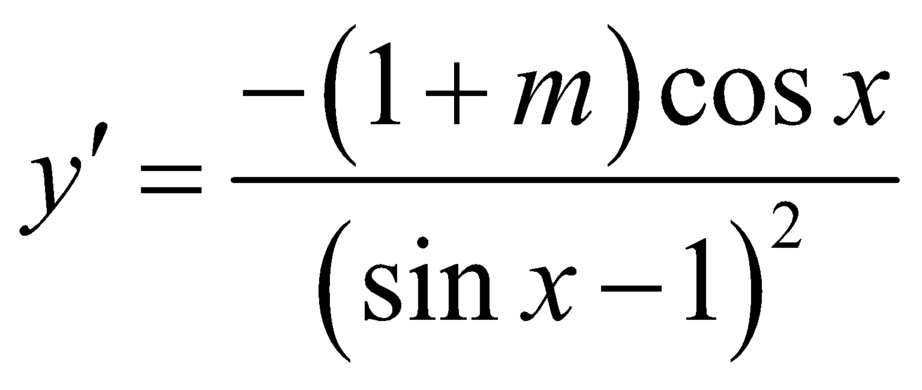
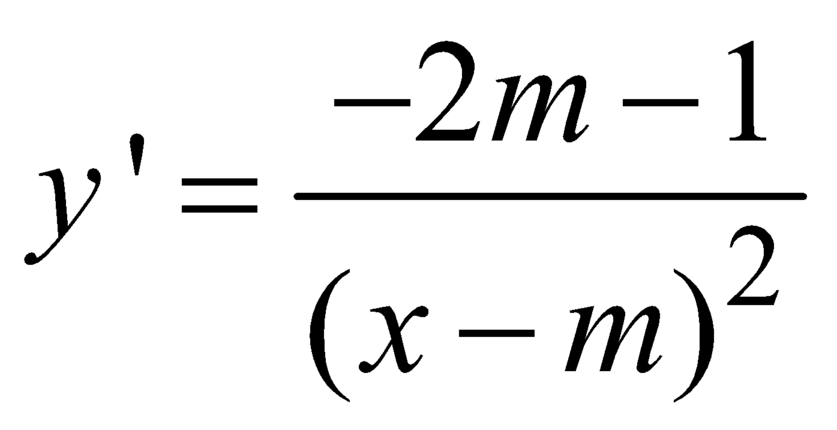
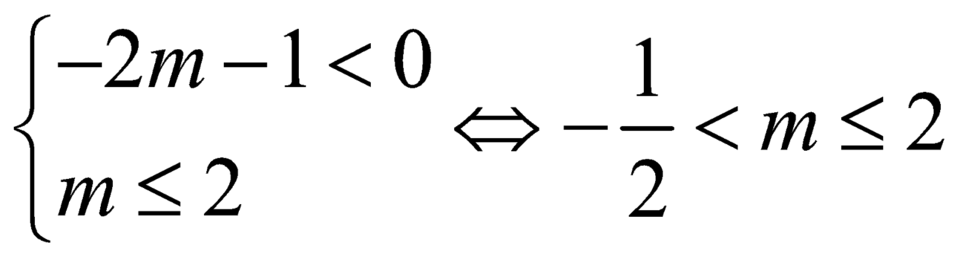
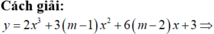
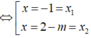
\(y'=\left(m^2-2\right)cosx-\dfrac{1}{cos^2x}\)
Để hàm số nghịch biến trên \(\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\Rightarrow y'\le0\) \(\forall x\in\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\)
Đặt \(cosx=t\Rightarrow0< t\le1\) \(\forall x\in\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\)
\(y'=\left(m^2-2\right)t-\dfrac{1}{t^2}\le0\) \(\Leftrightarrow m^2-2\le\dfrac{1}{t^3}\Leftrightarrow m^2\le\dfrac{1}{t^3}+2\) \(\forall t\in\text{(0;1]}\)
Đặt \(f\left(t\right)=\dfrac{1}{t^3}+2\Rightarrow m^2\le\min\limits_{\text{(0;1]}}f\left(t\right)\)
\(f'\left(t\right)=-\dfrac{3}{t^4}< 0\) \(\forall t\in\text{(0;1]}\) \(\Rightarrow f\left(t\right)\) nghịch biến \(\Rightarrow\min\limits_{\text{(0;1]}}f\left(t\right)=f\left(1\right)=3\)
\(\Rightarrow m^2\le3\Rightarrow-\sqrt{3}\le m\le\sqrt{3}\) \(\Rightarrow m=\left\{-1;0;1\right\}\)
\(\Rightarrow\) có 3 giá trị nguyên của m để hàm số nghịch biến trên \(\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\)