

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

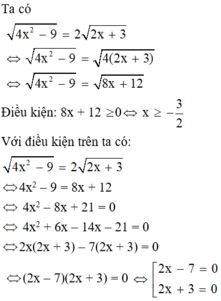


Ta có:
\(\Delta_1+\Delta_2+\Delta_3=a^2-4b+b^2-4c+c^2-4a=a^2+b^2+c^2-48\)
Dễ thấy:\(a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}=48\Rightarrow\Delta_1+\Delta_2+\Delta_3\ge0\)
Khi đó có ít nhất một phương trình có nghiệm

4. \(\sqrt{x}+\sqrt{y}=6\sqrt{55}\)
\(6\sqrt{55}\) là số vô tỉ, suy ra vế trái phải là các căn thức đồng dạng chứa \(\sqrt{55}\)
Đặt \(\sqrt{x}=a\sqrt{55};\sqrt{y}=b\sqrt{55}\) với \(a,b\in N\)
\(\Rightarrow a+b=6\)
Xét các TH:
a = 0 => b = 6
a = 1 => b = 5
a = 2 => b = 4
a = 3 => b = 3
a = 4 => b = 2
a = 5 => b = 1
a = 6 => b = 0
Từ đó dễ dàng tìm đc x, y

b/ \(\hept{\begin{cases}x^2+px+1=0\\x^2+qx+1=0\end{cases}}\)
Theo vi et ta có
\(\hept{\begin{cases}a+b=-p\\ab=1\end{cases}}\) và \(\hept{\begin{cases}c+d=-q\\cd=1\end{cases}}\)
Ta có: \(\left(a-c\right)\left(b-c\right)\left(a-d\right)\left(b-d\right)\)
\(=\left(c^2-c\left(a+b\right)+ab\right)\left(d^2-d\left(a+b\right)+ab\right)\)
\(=\left(c^2+cp+1\right)\left(d^2+dp+1\right)\)
\(=cdp^2+pcd\left(c+d\right)+p\left(c+d\right)+c^2d^2+\left(c+d\right)^2-2cd+1\)
\(=p^2-pq-pq+1+q^2-2+1\)
\(=p^2-2pq+q^2=\left(p-q\right)^2\)
a/ \(\hept{\begin{cases}x^2+2mx+mn-1=0\left(1\right)\\x^2-2nx+m+n=0\left(2\right)\end{cases}}\)
Ta có: \(\Delta'_1+\Delta'_2=\left(m^2-mn+1\right)+\left(n^2-m-n\right)\)
\(=m^2+n^2-mn-m-n+1\)
\(=\left(\frac{m^2}{2}-mn+\frac{n^2}{2}\right)+\left(\frac{m^2}{2}-m+\frac{1}{2}\right)+\left(\frac{n^2}{2}-n+\frac{1}{2}\right)\)
\(=\frac{1}{2}\left(\left(m-n\right)^2+\left(m-1\right)^2+\left(n-1\right)^2\right)\ge0\)
Vậy có 1 trong 2 phương trình có nghiệm

Đáp án A nhé!
Cái này áp dụng BĐT có si tí là ra ý mà, nếu k hiểu thì ib mik để mik làm nốt !
^_^
vì x2 luôn ko âm với mọi x
y2 luôn ko âm với mọi y
Áp dụng BĐ T cô si cho 2 số ko âm
=> x2 + 1/x2 >= 2 ( dấu = xảy ra khi x =1 ) (*)
CMTT
=> y2 + 1/y2 >= 2 ( dấu = xay ra khi y=1 ) (**)
Từ (*) và (**) ta có
x2 + y2 +1/x2 1/ y2 >= 4 ( dấu = xảy ra khi x=y=1)
nên để thoả mãn đẳng thức đề bài cho thì x=y=1

a) Phương trình 1,5x2 – 1,6x + 0,1 = 0
Có a + b + c = 1,5 – 1,6 + 0,1 = 0 nên x1 = 1; x2 = \(\dfrac{0,1}{15}\)
c) \(\left(2-\sqrt{3}\right)x^2+2\sqrt{3x}-\left(2+\sqrt{3}\right)=0\)
Có \(a+b+c=2-\sqrt{3}+2\sqrt{3}-\left(2+\sqrt{3}\right)=0\)
Nên x1 = 1, x2 = \(\dfrac{-\left(2+\sqrt{3}\right)}{2-\sqrt{3}}\) = -(2 + \(\sqrt{3}\))2 = -7 - 4\(\sqrt{3}\)
d) (m – 1)x2 – (2m + 3)x + m + 4 = 0
Có a + b + c = m – 1 – (2m + 3) + m + 4 = 0
Nên x1 = 1, x2 = \(\dfrac{m+4}{m-1}\)
a) Phương trình 1,5x2 – 1,6x + 0,1 = 0
Có a + b + c = 1,5 – 1,6 + 0,1 = 0 nên x1 = 1; x2 =
b) Phương trình √3x2 – (1 - √3)x – 1 = 0
Có a – b + c = √3 + (1 - √3) + (-1) = 0 nên x1 = -1, x2 = =
c) (2 - √3)x2 + 2√3x – (2 + √3) = 0
Có a + b + c = 2 - √3 + 2√3 – (2 + √3) = 0
Nên x1 = 1, x2 = = -(2 + √3)2 = -7 - 4√3
d) (m – 1)x2 – (2m + 3)x + m + 4 = 0
Có a + b + c = m – 1 – (2m + 3) + m + 4 = 0
Nên x1 = 1, x2 =