K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CT
8
P
3
HG
3
22 tháng 8 2017
Trong toán học, số hữu tỉ là các số x có thể biểu diễn dưới dạng phân số (thương) a/b, trong đó a và b là các số nguyên nhưng b {\displaystyle \neq }
Một cách tổng quát:
{\displaystyle \mathbb {Q} =\left\{x|x={\frac {m}{n}};m\in \mathbb {Z} ,n\in \mathbb {Z^{*}} \right\}}
Tập hợp số hữu tỉ là tập hợp đếm được.
Các số thực không phải là số hữu tỉ được gọi là các số vô tỉ.
Tuy nhiên, tập hợp các số hữu tỷ không hoàn toàn đồng nhất với tập hợp các phân số p/q,vì mỗi số hữu tỷ có thể biểu diễn bằng nhiều phân số khác nhau. Chẳng hạn các phân số 1/3,2/6,3/9... cùng biểu diễn một số hữu tỷ.
22 tháng 8 2017
số hữu tỉ là số viết đc dưới dạng phân số a/b với a,b\(\in\)Z, b\(\ne\)0
tập hợp các số hữu tỉ đc kí hiệu là Q
tk cho mk nha bn
22 tháng 8 2016
\(\frac{2008}{2009};\frac{20}{19}\)
\(1-\frac{2008}{2009}=\frac{1}{2009}\)
\(1-\frac{20}{19}=\frac{-1}{19}=\frac{1}{19}\)
Vì 19 < 2009 Nên \(\frac{1}{2009}< \frac{1}{19}\)
Vậy \(\frac{2008}{2009}>\frac{20}{19}\)
AH
Akai Haruma
Giáo viên
31 tháng 7 2023
Lời giải:
a. $x$ là số dương khi mà $x=\frac{3a-2}{4}>0$
$\Rightarrow 3a-2>0$
$\Rightarrow a> \frac{2}{3}$
b.
$x$ là số âmkhi mà $x=\frac{3a-2}{4}<0$
$\Rightarrow 3a-2<0$
$\Rightarrow a< \frac{2}{3}$
c. $x$ không âm không dương
Tức là $x=\frac{3a-2}{4}=0$
Hay $a=\frac{2}{3}$
31 tháng 7 2023
a) Để \(X=\dfrac{3a-2}{4}\) là số dương
\(\Rightarrow3a-2\) lớn hơn 0 ( 4 là số dương)
\(\Rightarrow a\) lớn hơn \(\dfrac{2}{3}\)
b) Để \(X=\dfrac{3a-2}{4}\) là số âm
\(\Rightarrow3a-2\) nhỏ hơn 0 (vì 4 là số dương)
\(\Rightarrow a\) nhỏ hơn \(\dfrac{2}{3}\)
c) Để X không dương không âm
\(3a-2=0\)
\(\Rightarrow a=\dfrac{2}{3}\)
4 tháng 9 2016
Gọi số hữu tỉ cần tìm là \(\frac{a}{9}\left(a\in Z\right)\)
Ta có: \(\begin{cases}-\frac{4}{9}< \frac{a}{9}\\\frac{a}{9}< -\frac{3}{5}\end{cases}\)=> \(\begin{cases}-4< a\\5.a< -3.9\end{cases}\)=> \(\begin{cases}-4< a\\5.a< -27\end{cases}\)=> \(\begin{cases}-4< a\\a< -5\end{cases}\), vô lí
Vậy không tìm được số hữu tỉ nào thỏa mãn đề bài
Số hữu tỉ là số viết được dưới dạng phân số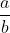
( a,b thuộc Z , b khác 0 )
Ký hiệu tập hợp các số hữu tỉ là
Trong toán học, số hữu tỉ là các số x có thể biểu diễn dưới dạng phân số (thương) a/b, trong đó a và b là các số nguyên với b
0. Tập hợp số hữu tỉ ký hiệu là 
.
Một cách tổng quát:
Tập hợp số hữu tỉ là tập hợp không đếm được.
Các số thực không phải là số hữu tỉ được gọi là các số vô tỉ.
Tuy nhiên, tập hợp các số hữu tỷ không hoàn toàn đồng nhất với tập hợp các phân số p/q, vì mỗi số hữu tỷ có thể biểu diễn bằng nhiều phân số khác nhau. Chẳng hạn các phân số 1/3, 2/6, 3/9,... cùng biểu diễn một số hữu tỷ.