

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Ta có ![]() với mọi
với mọi ![]()
Xét ![]() có
có ![]()
TH1: ![]()
khi đó ![]() nên ta có
nên ta có ![]() ,
,![]()
Suy ra ![]() .
.
TH2: 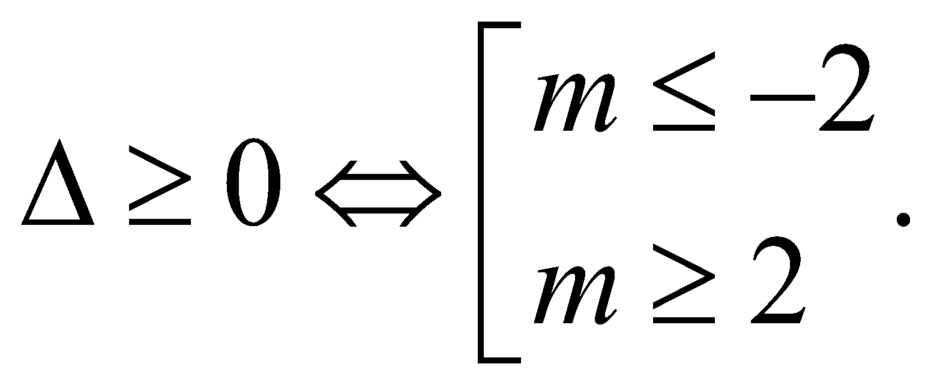
Nếu ![]() thì
thì ![]() nên không thỏa
nên không thỏa ![]() với mọi
với mọi ![]()
Nếu ![]() thì
thì ![]() với mọi
với mọi ![]() và
và ![]() có 2 nghiệm âm .
có 2 nghiệm âm .
Do đó ![]() ,
,![]() .
.
Suy ra ![]() .
.
Vậy ta có: ![]() nên có 10 giá trị nguyên của m.
nên có 10 giá trị nguyên của m.


Vậy có 8 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đáp án D

Đơn giản là hãy đặt \(\sqrt{6-x}=t\ge0\)
Do x và t nghịch biến nhau nên \(y=f\left(x\right)\) đồng biến trên \(\left(-8;5\right)\) đồng nghĩa \(y=f\left(t\right)\) nghịch biến trên \(\left(1;\sqrt{14}\right)\) (tại sao lại cho con số này nhỉ, (-10;5) chẳng hạn có tốt ko?)
\(\Leftrightarrow\left\{{}\begin{matrix}f'\left(t\right)\le0\\t+m=0\text{ vô nghiệm trên (0;\sqrt{14})}\end{matrix}\right.\)
\(\Leftrightarrow...\)