OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

Mini game 20/11 tri ân thầy cô, nhận thưởng hấp dẫn - Tham gia ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
6 tháng 3 2018
Cho hàm số y = x 3 - 2 x 2 - 1  (1) và các mệnh đề(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3(4) Cực trị của hàm số (1) là x = 0 và x = 4/3Trong các mệnh đề trên, số mệnh đề sai là: A. 0 B. 1 C. 2 D....
Đọc tiếp

Cho hàm số y = x 3 - 2 x 2 - 1  (1) và các mệnh đề

(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3

(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3

(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3

(4) Cực trị của hàm số (1) là x = 0 và x = 4/3

Trong các mệnh đề trên, số mệnh đề sai là:

A. 0

B. 1

C. 2

D. 3
#Toán lớp 12
1
CM
Cao Minh Tâm
6 tháng 3 2018

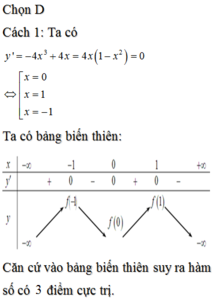
Chọn D

Ta có:  y ' = 3 x 2 - 4 x , y ' ' = 6 x - 4 ;

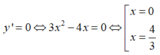
Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

y''(0) = -4 < 0; y''(4/3) = 4 > 0. Do đó hàm số có hai cực trị là x = 0 và x = 4/3

Các mệnh đề (1); (2) và (3) sai;mệnh đề (4) đúng.

Đúng(0)
PT
Pham Trong Bach
7 tháng 3 2018

Cho hàm số y = f ( x ) có đạo hàm trên R là f ' ( x ) = ( x - 2018 ) ( x - 2019 ) ( x - 2020 ) 4 . Hàm số đã cho có bao nhiêu điểm cực trị?

A. 2

B. 1

C. 4

D. 3
#Toán lớp 12
1
CM
Cao Minh Tâm
7 tháng 3 2018

Đúng(0)
PT
Pham Trong Bach
11 tháng 6 2019

Cho hàm số y = f(x)  có đạo hàm trên R. Đồ thị hàm số y= f’(x)  như hình vẽ bên dưới

Description: 88

Số điểm cực trị của hàm số  y= g( x)= f( x- 2017) – 2018x+ 2019 là

A. 1

B. 2

C.3

D. 4
#Toán lớp 12
1
CM
Cao Minh Tâm
11 tháng 6 2019

Dựa vào đồ thị hàm số y= f’(x)  suy ra phương trình f’( x- 2017) = 2018  có 1 nghiệm đơn duy nhất. 

 

Suy ra hàm số y= g( x)  có 1 điểm cực trị

Đúng(1)
PT
Pham Trong Bach
23 tháng 4 2017
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ . Đồ thị hàm số y = f'(x) được cho như hình vẽ bên. Số điểm cực trị của hàm số g(x) = f(x-2017) - 2018x + 2019 là:  A. 1. B. 3. C. 2. D....
Đọc tiếp

Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ . Đồ thị hàm số y = f'(x) được cho như hình vẽ bên.

Số điểm cực trị của hàm số g(x) = f(x-2017) - 2018x + 2019 là: 

A. 1.

B. 3.

C. 2.

D. 0.
#Toán lớp 12
1
CM
Cao Minh Tâm
23 tháng 4 2017

Chọn A

Ta có: g(x) = f(x-2017) - 2018x + 2019.

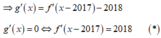
Nhận xét: tịnh tiến đồ thị hàm số y = f'(x) sang bên phải theo phương của trục hoành 2017 đơn vị ta được đồ thị hàm số y = f'(x-2017) . Do đó, số nghiệm của phương trình f'(x) = 2018 bằng số nghiệm của phương trình (*).

Dựa vào đồ thị ta thấy phương trình (*) có nghiệm đơn duy nhất hay hàm số đã cho có duy nhất 1 điểm cực trị.

Đúng(0)
PT
Pham Trong Bach
7 tháng 10 2018
Cho hàm số y= f( x) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 Số điểm cực trị của hàm số  f x   là A. 5 B. 3 C. 1...
Đọc tiếp

Cho hàm số y= f( x) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 Số điểm cực trị của hàm số  f x   là

A. 5

B. 3

C. 1

D. 2
#Toán lớp 12
1
CM
Cao Minh Tâm
7 tháng 10 2018

 

 

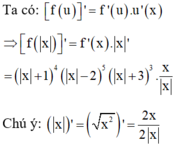
Do đó hàm số f(|x|)  có 3 điểm cực trị  tại x= 2; x= -2 và  x= 0

Chọn B.

Đúng(0)
KN
kim ngân
2 tháng 9 2021

cho hàm số y=f(x) có f'(x) = (x-2021)^5 * (x-2020)^2020 * (x-2019)^2019. Hàm số f(x) có bao nhiêu điểm cực trị ?

 
#Toán lớp 12
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2021

\(f'\left(x\right)=0\) có 2 nghiệm bội lẻ \(x=2019\) và \(x=2021\) nên hàm có 2 cực trị

Đúng(0)
S
Shuu
22 tháng 8 2021
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m làCâu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất  cả các giá trị thực của  m để hàm  số có 3 cực...
Đọc tiếp

Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là

Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất  cả các giá trị thực của  m để hàm  số có 3 cực trị
#Toán lớp 12
0
PT
Pham Trong Bach
30 tháng 11 2017
Cho hàm số liên tục trên khoảng (a;b) và x 0   ∈   ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 )   =   0 . (2) Nếu hàm số y   =   f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn...
Đọc tiếp

Cho hàm số liên tục trên khoảng (a;b) và x 0   ∈   ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?

(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 )   =   0 .

(2) Nếu hàm số y   =   f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 )   =   f ' ' ( x 0 )   =   0 thì điểm  x 0 không phải là điểm cực trị của hàm số  y   =   f ( x ) .

(3) Nếu f'(x) đổi dấu khi x qua điểm  x 0 thì điểm  x 0 là điểm cực tiểu của hàm số  y   =   f ( x ) .

(4) Nếu hàm số  y   =   f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm  x 0 thỏa mãn điều kiện f ' ( x 0 )   =   0 ,   f ' ' ( x 0   )   >   0 thì điểm  x 0 là điểm cực tiểu của hàm số y   =   f ( x ) .

A. 1

B. 2

C. 0

D. 3
#Toán lớp 12
1
CM
Cao Minh Tâm
30 tháng 11 2017

Đáp án A

Phương pháp:

Dựa vào khái niệm cực trị và các kiến thức liên quan.

Cách giải:

(1) chỉ là điều kiện cần mà không là điều kiện đủ.

VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.

(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.

(3) hiển nhiên sai.

Vậy (1), (2), (3): sai; (4): đúng

Đúng(0)
LV
Lê vsbzhsjskskskssm
24 tháng 7 2021

độ dài AB là 2 điểm cực trị của hàm số y=(x+1).(x-2)² là 

A)5✓2

B)2

C)2✓5

D)4

 
#Toán lớp 12
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021

\(y'=\left(x-2\right)^2+2\left(x+1\right)\left(x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=4\\x=2\Rightarrow y=0\end{matrix}\right.\)

\(\Rightarrow A\left(0;4\right)\) ; \(B\left(2;0\right)\)

\(\Rightarrow\overrightarrow{AB}=\left(2;-4\right)\Rightarrow AB=\sqrt{2^2+\left(-4\right)^2}=2\sqrt{5}\)

Đúng(1)
PT
Pham Trong Bach
11 tháng 1 2017

Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x - 2 ) ( x 2 - 3 ) ( x 4 - 9 ) . Số điểm cực trị của hàm số y = f ( x ) là

A. 3

B. 4

C. 2

D. 1
#Toán lớp 12
1
CM
Cao Minh Tâm
11 tháng 1 2017

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP