Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)12a<15a
Ta có:12<15 để có bất đẳng thức
12a<15a ta phải nhân cả 2 vế của bất đẳng thức 12<15 vs số a
Để đc bất đẳng thức cùng chiều thì a<0
b)4a<3a
Vì 4>3 và 4a<3a trái chiều.Để nhân 2 vế của bất đẳng thức 4>3 vs a đc bất đẳng thức trái chiều thì a<0
c)-3a>-5a
Từ -3 > -5 để có -3a > -5a thì a phải là số dương

a. Ta có: a > b ⇔ 3a > 3b ⇔ 3a + 5 > 3b + 5 (1)
Mặt khác: 3b + 5 > 3b + 2 (2)
Từ (1) và (2) suy ra: 3a + 5 > 3b + 2
b. Ta có: a > b ⇔ -4a < -4b ⇔ 3 – 4a < 3 – 4b (1)
Mặt khác: 2 – 4a < 3 – 4a (2)
Từ (1) và (2) suy ra: 2 – 4a < 3 – 4b
a. Ta có: a > b ⇔ 3a > 3b ⇔ 3a + 5 > 3b + 5 (1)
Mặt khác: 3b + 5 > 3b + 2 (2)
Từ (1) và (2) suy ra: 3a + 5 > 3b + 2
b. Ta có: a > b ⇔ -4a < -4b ⇔ 3 – 4a < 3 – 4b (1)
Mặt khác: 2 – 4a < 3 – 4a (2)
Từ (1) và (2) suy ra: 2 – 4a < 3 – 4b

a) Từ a + 5 < b + 5
=> a + 5 + (-5) < b + 5 + (-5) (cộng hai vế với -5)
=> a < b
a)từ a+5<b+5 ta cộng -5 vào 2 vế được a<b
b)từ -3a>-3b ta nhân 2 vế với -1/3 (tức là chia cả 2 vế cho -3) và -3a . -1/3< -3b . -1/3 sẽ được a<b

Ta có: BĐT phụ sau: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{9}{a+b+c}\)( CM bằng BĐT Shwars nha).Áp dụng ta có:
\(\frac{1}{a+3b+5c}+\frac{1}{b+3c+5a}+\frac{1}{3a+2b+4c}\ge\frac{9}{9a+6b+12c}=\frac{3}{3a+2b+4c}\left(1\right)\)
\(\frac{1}{b+3c+5a}+\frac{1}{c+3a+5b}+\frac{1}{3b+2c+4a}\ge\frac{9}{9b+6c+12a}=\frac{3}{3b+2c+4a}\left(2\right)\)
\(\frac{1}{c+3a+5b}+\frac{1}{a+3b+5c}+\frac{1}{3c+2a+4b}\ge\frac{9}{9c+6a+12b}=\frac{3}{3c+2a+4b}\left(3\right)\)
Cộng (1),(2) và (3) có:
\(2\left(\frac{1}{a+3b+5c}+\frac{1}{b+3c+5c}+\frac{1}{c+3a+5b}\right)+\left(\frac{1}{3a+2b+4c}+\frac{1}{3b+2c+4a}+\frac{1}{3c+2a+4b}\right)\ge3\left(\frac{1}{3a+2b+4c}+\frac{1}{3b+2c+4a}+\frac{1}{3c+2a+4b}\right)\)
\(\Rightarrow2VP\ge2VT\)
\(\RightarrowĐPCM\)

1/ 2a + 2b = 2( a + b )
2/ 3a - 6b - 9c = 3( a - 2b - 3c )
3/ 5ax - 15ay + 20a = 5a( x - 3y + 4 )
4/ 3a2x - 6a2y + 12a = 3a( ax - 2ay + 4 )
5/ 4a( x - 5 ) - 2( 5 - x ) = 4a( x - 5 ) + 2( x - 5 ) = ( x - 5 )( 4a + 2 ) = ( x - 5 )2( 2a + 1 )
6. -3a( x - 3 ) + ( 3 - x ) = 3a( 3 - x ) + 1( 3 - x ) = ( 3a + 1 )( 3 - x )
7/ xm+1 - xm = xm( x + 1 )
8/ xm+2 - x2 = x2( xm - 1 )

a: 5b>3b
nên 5b-3b>0
=>2b>0
hay b>0
b: -12b>8b
nên -20b>0
hay b<0
c: -6b>=9b
nên -6b-9b>=0
=>b<=0
d: 3b<=15b
=>3b-15b<=0
=>-12b<=0
hay b>=0
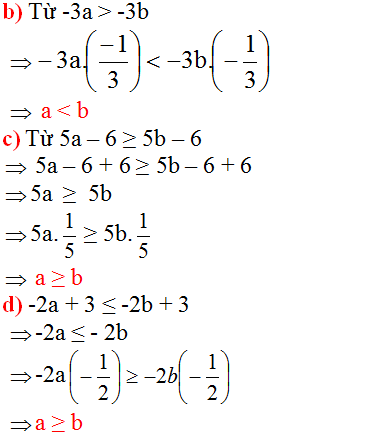
a) Ta có: 12 < 15. Để có bất đẳng thức
12a < 15a ta phải nhân cả hai vế của bất đẳng thức 12 < 15 với số a.
Để được bất đẳng thức cùng chiều thì a > 0
b) Vì 4 > 3 và 4a < 3a trái chiều. Để nhân hai vế của bất đẳng thức 4 > 3 với a được bất đẳng thức trái chiều thì a < 0
c) Từ -3 > -5 để có -3a > -5a thì a phải là số dương