Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(X \rightarrow _{-1}^{\ \ 0}e+Y\)
Từ phương trình phóng xạ => Cứ 1 hạt nhân \(X\) bị phóng xạ thì tạo thành 1 hạt nhân \(\beta^-\)
Số hạt nhân \(X\) bị phóng xạ là \(\Delta N = 4,2.10^{13}\) hạt. (1)
Số hạt nhân ban đầu \(X\) (trong 1 gam) là: \(N_0 = \frac{m_0}{A}.N_A= \frac{1}{58,933}.6,023.10^{23} \approx 1,022.10^{22}\)hạt. (2)
Từ (1) và (2) => \(\Delta N = N_0(1-2^{-\frac{t}{T}})\)
=> \(2 ^{-t/T}=1- \frac{\Delta N}{N_0} \)
=> \(\frac{-t}{T} = \ln_2(1- \frac{4,2.10^{13}}{1,022.10^{22}}) =- 5,93.10^{-9}\)
=> \(T \approx 1,68.10^{8}s.\) (\(t = 1s\))
Chọn đáp án.B.1,68.108s.
Sau thời gian t1 số hạt nhân còn lại là
\(N = N_0 2^{-\frac{t}{T}}\)=> \(\frac{N}{N_0}= 0,2= 2^{-\frac{t_1}{T}}=> t_1 = -T.\ln_20,2.\)
Sau thời điểm t2 thì số hạt nhân còn lại là
\(N_1 = N_0 2^{-\frac{t_2}{T}}=> \frac{N}{N_0} = 0,05 = 2^{-\frac{t_2}{T}}\)=> \(t_2 = -T\ln_20,05.\)
Mà \(t_2 = t_1 +100\)
=> \(-T \ln_2 0,05 = -T\ln_2 0,2 + 100\)
=> \(T = \frac{100}{\ln_2{(0,2/0,05)}}=50 s. \)
Đáp án C:
Sau quá trình bắn phá Mn55 bằng nơtron kết thúc thì số nguyên tử của Mn56 giảm, cò số nguyên tử Mn55 không đổi, Sau 10 giờ = 4 chu kì số nguyên tử của Mn56 giảm 24 = 16 lần. Do đó thì tỉ số giữa nguyên tử của hai loại hạt trên là:
Đồng vị phóng x
Đáp án B
Phương pháp:Áp dụng định luật phóng xạ ánh sáng
Cách giải: Đáp án B
Số nguyên tử 
sau khi ngừng quá trình bắn phá
là không thay đổi,chỉ có số nguyên tử 
phóng xạ thay đổi theo thời gian.
Ngay khi quá trình bắn phá kết thúc (t =0), số nguyên tử
là
N
1
,số nguyên tử 
là N0,
ta có ta có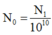 
Sau t = 10h =4T, số nguyên tử 
cònlại là
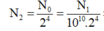
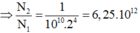
Độ phóng xạ sau 38,1 giờ là
\(H = H_0 2^{-\frac{t}{T}}\)
=> \(\frac{H}{H_0}= 2^{-\frac{t}{T}}= 2^{-\frac{38,1}{12,7}}=0, 125.\)
Tức là độ phóng xạ của đồng vị sau 38,1 giờ thì chiếm 12,5 % so với độ phóng xạ ban đầu.
- So với số hạt nhân ban đầu, sau khoảng thời gian t = 2τ số hạt nhân nguyên tử của chất phóng xạ còn lại chiếm:
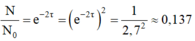
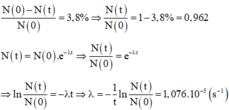
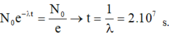
Đáp án A.
Theo bài:
N 0 - N t N 0 = 3 , 8 % ⇒ N t N 0 = 1 - 3 , 8 % = 0 , 962 N t = N 0 . e - λ t ⇒ N t N 0 = e - λ t ⇒ ln N t N 0 = - λ t ⇒ λ = - 1 t ln N t N 0 = 1 , 076 . 10 - 5 ( s - 1 )