
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\sqrt{14-6\sqrt{5}}=\sqrt{\left(3-\sqrt{5}\right)^2}=3-\sqrt{5}\)
b, c) tương tự câu a.
d) \(\left(3-\sqrt{2}\right)\sqrt{11+6\sqrt{2}}\)
\(=\left(3-\sqrt{2}\right)\sqrt{\left(3+\sqrt{2}\right)^2}\)
\(=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)\)
\(=9-2\)
\(=7\)
e) \(\sqrt{11-6\sqrt{2}+\sqrt{3-2\sqrt{2}}}\)
\(=\sqrt{11-6\sqrt{2}+\sqrt{\left(1-\sqrt{2}\right)^2}}\)
\(=\sqrt{11-6\sqrt{2}+\sqrt{2}-1}\)
\(=\sqrt{10-5\sqrt{2}}\)

\(\dfrac{-2m+1}{2}=1-2m\) \(\Leftrightarrow\) m=\(\dfrac{1}{2}\).
\(\dfrac{m-1}{2}=m-1\) \(\Leftrightarrow\) m=1.
Hai phương trình đã cho không là hai phương trình tương đương.

\(\left(\sqrt{7}+\sqrt{6}\right)^2+\sqrt{168}\)
\(=7+6+2\sqrt{42}+2\sqrt{42}=13+4\sqrt{42}\)

a) Ta có: \(\sqrt{11+6\sqrt{2}}-\left(3+\sqrt{2}\right)\)
\(=3+\sqrt{2}-3-\sqrt{2}\)
=0
b) Ta có: \(\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{16}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{6}+\sqrt{8}+\sqrt{4}}{\sqrt{2}+\sqrt{3}+2}\)
\(=\sqrt{2}+1\)

5.
\(\Delta=\left(-2\right)^2-4\left(-15\right)=64\)
6.
\(\Delta'=2^2-5.\left(-7\right)=39\)
Mà thầy ơi em hok hiểu khúc đầu làm sao để ra cái đó ròi ra kết quả á :((( cả 2 câu lun

ĐKXĐ: \(x\ge0;x\ne1\)
\(\frac{15\sqrt{x}-11}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}+\frac{3\sqrt{x}-2}{\sqrt{x}-1}-\frac{3}{\sqrt{x}+3}\)
\(=\frac{15\sqrt{x}-11}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}+\frac{\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}-\frac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{15\sqrt{x}-11+3x+7\sqrt{x}-6-3\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{3x+19\sqrt{x}-14}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}=\frac{\left(\sqrt{x}+7\right)\left(3\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)

\(\sqrt{a+2016}\)- \(\sqrt{a+2013}\) = (\(\sqrt{a+2016}\)- \(\sqrt{a+2013}\)) . (\(\sqrt{a+2016}+\)\(\sqrt{a+2013}\)) / \(\sqrt{a+2016}+\)\(\sqrt{a+2013}\)[ nhân cả tử và mẫu với (\(\sqrt{a+2016}+\)\(\sqrt{a+2013}\)), (mẫu cũ =1) ]
= (a+2016)-(a+2013)/\(\sqrt{a+2016}+\)\(\sqrt{a+2013}\)
k mk nha
\(\frac{\left(a+2016\right)-\left(a+2013\right)}{\sqrt{a+2016}+\sqrt{a+2013}}\)\(=\frac{\left(\sqrt{a+2016}\right)^2-\left(\sqrt{a+2013}\right)^2}{\sqrt{a+2016}+\sqrt{a+2013}}=\frac{\left(\sqrt{a+2016}+\sqrt{a+2013}\right)\left(\sqrt{a+2016}-\sqrt{a-2013}\right)}{\sqrt{a+2016}+\sqrt{a+2013}}\)
\(=\sqrt{a+2016}-\sqrt{a+2013}\)

a: \(\Leftrightarrow\sqrt{6}\left(x+1\right)=5\sqrt{6}\)
=>x+1=5
=>x=4
b: =>x^2/10=1,1
=>x^2=11
=>x=căn 11 hoặc x=-căn 11
c: =>(4x+3)/(x+1)=9 và (4x+3)/(x+1)>=0
=>4x+3=9x+9
=>-5x=6
=>x=-6/5
d: =>(2x-3)/(x-1)=4 và x-1>0 và 2x-3>=0
=>2x-3=4x-4 và x>=3/2
=->-2x=-1 và x>=3/2
=>x=1/2 và x>=3/2
=>Ko có x thỏa mãn
e: Đặt căn x=a(a>=0)
PT sẽ là a^2-a-5=0
=>\(\left[{}\begin{matrix}a=\dfrac{1+\sqrt{21}}{2}\left(nhận\right)\\a=\dfrac{1-\sqrt{21}}{2}\left(loại\right)\end{matrix}\right.\)
=>x=(1+căn 21)^2/4=(11+căn 21)/2
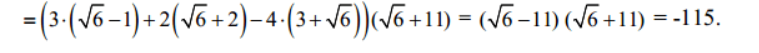
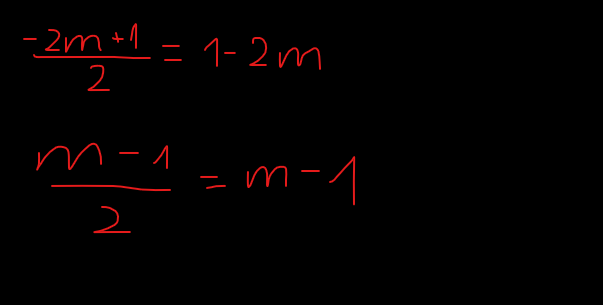

\(3\left(\sqrt{6}-1\right)+2\left(\sqrt{6}+2\right)-4\left(3+\sqrt{6}\right)\)
\(=3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}=\sqrt{6}-11\)