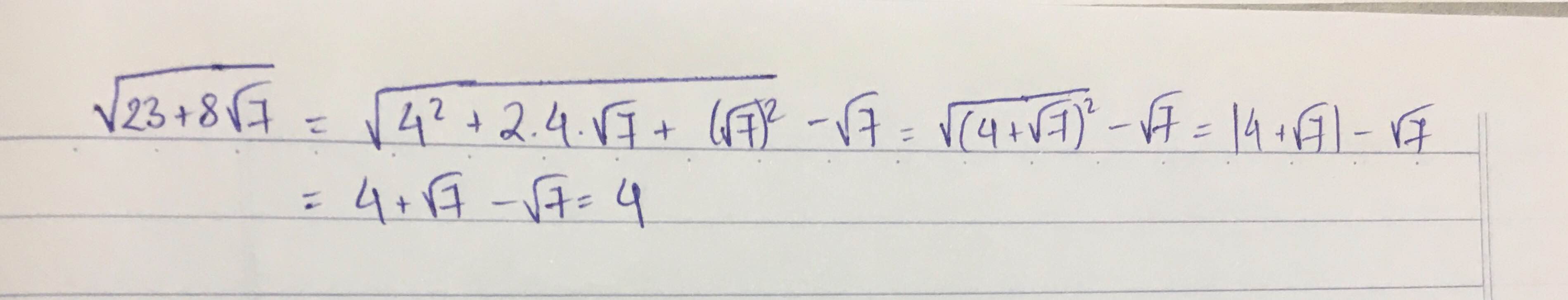
Rút gọn: \(\sqrt{23+8\sqrt{7}}-\sqrt{7}\)giải gấp giúp e nha

LT

Lê Thị Khánh Huyền

24 tháng 7 2020 - olm

Rút gọn:

D=\(\sqrt{11-6\sqrt{2}}-3+\sqrt{2}\)

E=\(\sqrt{23+8\sqrt{7}}-\sqrt{7}\)

#Toán lớp 9

1

KA

Kiyotaka Ayanokoji

24 tháng 7 2020

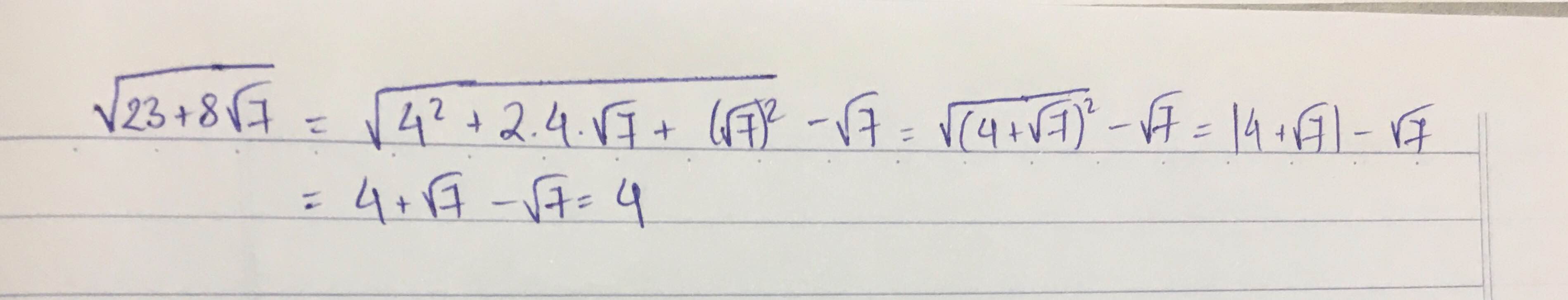
Trả lời:

\(D=\sqrt{11-6\sqrt{2}}-3+\sqrt{2}\)

\(D=\sqrt{9-6\sqrt{2}+2}-3+\sqrt{2}\)

\(D=\sqrt{\left(3-\sqrt{2}\right)^2}-3+\sqrt{2}\)

\(D=3-\sqrt{2}-3+\sqrt{2}\)

\(D=0\)

\(E=\sqrt{23+8\sqrt{7}}-\sqrt{7}\)

\(E=\sqrt{16+8\sqrt{7}+7}-\sqrt{7}\)

\(E=\sqrt{\left(4+\sqrt{7}\right)^2}-\sqrt{7}\)

\(E=4+\sqrt{7}-\sqrt{7}\)

\(E=4\)

Đúng(0)

LT

Lê Thanh Nhã Vi

24 tháng 6 2019 - olm

rút gọn biểu thức:

\(\sqrt{8-2\sqrt{7}}-\sqrt{23-8\sqrt{7}}\)

#Toán lớp 9

5

TN

Thanh Ngân

24 tháng 6 2019

\(\sqrt{8-2\sqrt{7}}-\sqrt{23-8\sqrt{7}}=\) \(\sqrt{1-2\sqrt{7}+7}-\sqrt{7-2.4.\sqrt{7}+16}\)

\(=\sqrt{\left(1-\sqrt{7}\right)^2}-\sqrt{\left(\sqrt{7}-4\right)^2}\)

\(=\sqrt{7}-1-\left(-\sqrt{7}+4\right)\)

\(=\sqrt{7}-1+\sqrt{7}-4\)\(=2\sqrt{7}-5\)

chúc bn học tốt

Đúng(0)

MM

•๖ۣۜMã ๖ۣۜMã ( ๖ۣۜTεαм ๖ۣۜTαм ๖ۣۜGĭ...

24 tháng 6 2019

=\(\sqrt{\left(\sqrt{7}-1\right)^2}\)- \(\sqrt{\left(4-\sqrt{7}\right)^2}\)

= \(\sqrt{7}\)- 1 - 4 + \(\sqrt{7}\)

= \(2\sqrt{7}\)-5

đ/á ra hơi kì

#mã mã#

Đúng(0)

KM

Khánh Minh Nguyễn

14 tháng 8 2020 - olm

Rút gọn:

A = \(\frac{\sqrt{7+\sqrt{5}}+\sqrt{7-\sqrt{5}}}{7+2\sqrt{11}}-\sqrt{3-2\sqrt{2}}\)

Giải chi tiết giúp mik nha

#Toán lớp 9

1

F

FL.Hermit

14 tháng 8 2020

Đặt: \(B=\sqrt{7+\sqrt{5}}+\sqrt{7-\sqrt{5}}\)

=> \(B^2=7+\sqrt{5}+7-\sqrt{5}+2\sqrt{\left(7+\sqrt{5}\right)\left(7-\sqrt{5}\right)}\)

=> \(B^2=14+2\sqrt{49-5}\)

=> \(B^2=14+2\sqrt{44}\)

=> \(A=\frac{\sqrt{14+4\sqrt{11}}}{7+2\sqrt{11}}-\sqrt{\left(\sqrt{2}-1\right)^2}\)

=> \(A=\sqrt{\frac{2}{7+2\sqrt{11}}}-\left(\sqrt{2}-1\right)\)

=> \(A=\sqrt{\frac{2}{7+2\sqrt{11}}}-\sqrt{2}+1\)

ĐỀ BÀI CHẮC SAI RỒI PHẢI DƯỚI MẪU PHẢI LÀ \(\sqrt{7+2\sqrt{11}}\) THÌ LÚC ĐÓ BIỂU THỨC A RA ĐẸP HƠN !!!!

NẾU SỬA ĐỀ BÀI NHƯ TRÊN:

=> \(A=\frac{\sqrt{2}.\sqrt{7+2\sqrt{11}}}{\sqrt{7+2\sqrt{11}}}-\left(\sqrt{2}-1\right)\)

=> \(A=\sqrt{2}-\sqrt{2}+1\)

=> \(A=1\)

ĐÓ BÂY GIỜ RA A = 1 RẤT ĐẸP

Đúng(0)

PH

Phan Hoàng Hải

4 tháng 8 2021

rút gọn

\(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right).\sqrt{7}+7\sqrt{8}\)

giúp mink vs ạ

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

4 tháng 8 2021

\(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right)\cdot\sqrt{7}+7\sqrt{8}\)

\(=\left(3\sqrt{7}-2\sqrt{14}\right)\cdot\sqrt{7}+14\sqrt{2}\)

\(=21-14\sqrt{2}+14\sqrt{2}\)

=21

Đúng(3)

PH

Phan Hoàng Hải

4 tháng 8 2021

thank

Đúng(0)

HP

Hà Phạm Như Ý

19 tháng 6 2017 - olm

Rút gọn
\(\sqrt{23+8\sqrt{7}}\)

#Toán lớp 9

2

PT

pham thi thu trang

19 tháng 6 2017

=\(\sqrt{4^2+2\times4\times\sqrt{7}+\left(\sqrt{7}\right)^2}\)

= \(\sqrt{\left(4+\sqrt{7}\right)^2}\)= \(4+\sqrt{7}\)

Đúng(0)

PH

Phạm Huỳnh Bích Duyên

19 tháng 6 2017

=\(\sqrt{4^2+2\times4\times\sqrt{7}+\left(\sqrt{7}\right)^2}\) =\(\left(\sqrt{4+\sqrt{7}}\right)^2\) =\(\left|4+\sqrt{7}\right|\) =\(4+\sqrt{7}\)

Đúng(0)

1N

123 nhan

21 tháng 7 2023

Rút gọn: (Giải chi tiết từng bước)

7) \(\left(\sqrt{28}-\sqrt{12}-\sqrt{7}\right)\sqrt{7}+2\sqrt{21}\)

8) \(\left(\sqrt{99}-\sqrt{18}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)

#Toán lớp 9

1

VL

Vui lòng để tên hiển thị

21 tháng 7 2023

`a, (sqrt 28 - sqrt 12 - sqrt 7) sqrt 7 + 2 sqrt 21`.

`= sqrt(28.7) - sqrt(12.7) - sqrt(7.7) + 2 sqrt 21`.

`= sqrt(4. 7.7) - sqrt (12.7) - 7 + 2 sqrt 21`.

`= 14 - sqrt(4.3.7) - 7 + 2 sqrt 21`.

`= 7`.

`b, (sqrt99-sqrt18-sqrt11)sqrt11+3sqrt22`

`= sqrt(99.11)- sqrt(18.11)-sqrt(11.11) +3sqrt22`

`= sqrt(9.11.11)-sqrt(2.9.11)-11+3sqrt22`

`= 33 - 11 = 22`.

Đúng(2)

1N

123 nhan

21 tháng 7 2023

Giỏi quá <3

Đúng(0)

TN

Trang Nguyễn

31 tháng 8 2021

1) rút gọn

A= \(3\sqrt{2}+5\sqrt{8}-2\sqrt{50}\)

B= \(\dfrac{1}{3+\sqrt{5}}+\dfrac{1}{3-\sqrt{5}}\)

C= \(\sqrt{7-4\sqrt{3}}+\sqrt{12+6\sqrt{3}}\)

Giúp mk vs ạ mk cần gấp

#Toán lớp 9

5

HP

Hồng Phúc

31 tháng 8 2021

\(A=3\sqrt{2}+5\sqrt{8}-2\sqrt{50}\)

\(=3\sqrt{2}+10\sqrt{2}-10\sqrt{2}\)

\(=3\sqrt{2}\)

Đúng(0)

HP

Hồng Phúc

31 tháng 8 2021

\(B=\dfrac{1}{3+\sqrt{5}}+\dfrac{1}{3-\sqrt{5}}\)

\(=\dfrac{3-\sqrt{5}}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}+\dfrac{3+\sqrt{5}}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}\)

\(=\dfrac{3-\sqrt{5}+3+\sqrt{5}}{9-5}\)

\(=\dfrac{3}{2}\)

Đúng(0)

LV

Lê Vũ Nhã Linh

5 tháng 12 2017 - olm

Các bạn giúp mình với!!!! Mình cần gấp lắm pleaseeeeee. Ai đúng mình tick cho.

Rút gọn :\(\sqrt{\frac{6\sqrt{7}-15}{\sqrt{7}-2}}+\sqrt{\frac{45-17\sqrt{7}}{3-\sqrt{7}}}\)

#Toán lớp 9

1

DT

Duong Thuc Hien

5 tháng 12 2017

= 1,41(đã làm tròn)

Đúng(0)

LT

Lê Thị Khánh Huyền

22 tháng 7 2020 - olm

Bài 1:Tìm x để bt có nghĩaa)\(\sqrt{\left(x-1\right)\left(x-3\right)}\)b) \(\sqrt{\frac{1-x}{x+2}}\)Bài 2:Rút gọna) A=\(\sqrt{\left(\sqrt{3}-1\right)^2-\sqrt{3}}\)d) D=\(\sqrt{23+8\sqrt{7}}-\sqrt{7}\)b) B= \(\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}\)c) C=\(\sqrt{7-4\sqrt{3}}+\sqrt{7+4\sqrt{3}}\)Huhu mọi người giúp e...

Đọc tiếp

#Toán lớp 9

4

MN

Minh Nguyen

28 tháng 7 2020

Bài 2 :

a) Sửa đề :

\(A=\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{3}\)

\(A=\sqrt{3}-1-\sqrt{3}\)

\(A=-1\)

b) \(B=\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}\)

\(B=\sqrt{\left(\sqrt{2}+1\right)^2}-\sqrt{\left(\sqrt{2}-1\right)^2}\)

\(B=\sqrt{2}+1-\sqrt{2}+1\)

\(B=2\)

c) \(C=\sqrt{7-4\sqrt{3}}+\sqrt{7+4\sqrt{3}}\)

\(C=\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{\left(2+\sqrt{3}\right)^2}\)

\(C=2-\sqrt{3}+2+\sqrt{3}\)

\(C=4\)

d) \(D=\sqrt{23+8\sqrt{7}}-\sqrt{7}\)

\(D=\sqrt{\left(4+\sqrt{7}\right)^2}-\sqrt{7}\)

\(D=4+\sqrt{7}-\sqrt{7}\)

\(D=4\)

Đúng(0)

MN

Minh Nguyen

28 tháng 7 2020

Bài 1 :

a) Để \(\sqrt{\left(x-1\right)\left(x-3\right)}\) có nghĩa

\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\ge0\)

TH1 :\(\hept{\begin{cases}x-1\ge0\\x-3\ge0\end{cases}\Leftrightarrow}\hept{\begin{cases}x\ge1\\x\ge3\end{cases}\Leftrightarrow x\ge3}\)

TH2 : \(\hept{\begin{cases}x-1\le0\\x-3\le0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le1\\x\le3\end{cases}\Leftrightarrow}x\le1}\)

Vậy để biểu thức có nghĩa thì \(\orbr{\begin{cases}x\ge3\\x\le1\end{cases}}\)

b) Để \(\sqrt{\frac{1-x}{x+2}}\)có nghĩa

\(\Leftrightarrow\frac{1-x}{x+2}\ge0\)

TH1 : \(\hept{\begin{cases}1-x\ge0\\x+2\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le1\\x\ge-2\end{cases}\Leftrightarrow}-2\le x\le1}\)

TH2 : \(\hept{\begin{cases}1-x\le0\\x+2\le0\end{cases}\Leftrightarrow}\hept{\begin{cases}x\ge1\\x\le-2\end{cases}\Leftrightarrow x\in\varnothing}\)

Vậy để biểu thức có nghĩa thì \(-2\le x\le1\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP