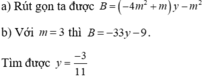Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(M=\dfrac{-y+4}{y-2}+\dfrac{1}{y-2}+\dfrac{3}{y+2}\)
\(=\dfrac{-y+5}{y-2}+\dfrac{3}{y+2}=\dfrac{-y^2-2y+5y+10+3y-6}{\left(y-2\right)\left(y+2\right)}\)
\(=\dfrac{-y^2+6y+4}{\left(y-2\right)\left(y+2\right)}\)
b: Khi y=3 thì \(M=\dfrac{-3^2+6\cdot3+4}{\left(3-2\right)\left(3+2\right)}=\dfrac{-5+18}{5}=\dfrac{13}{5}\)

\(M=\dfrac{4}{x+2}+\dfrac{3}{x-2}-\dfrac{5x+2}{x^2-4}\left(dkxd:x\ne\pm2\right)\)
\(=\dfrac{4}{x+2}+\dfrac{3}{x-2}-\dfrac{5x+2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4\left(x-2\right)+3\left(x+2\right)-\left(5x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4x-8+3x+6-5x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x-4}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2}{x+2}\)
Để \(M=\dfrac{2}{5}\) thì \(\dfrac{2}{x+2}=\dfrac{2}{5}\)
Suy ra :
\(2.5=2\left(x+2\right)\)
\(\Leftrightarrow2x+4=10\)
\(\Leftrightarrow x=3\)
Vậy \(M=\dfrac{2}{5}\) thì x = 3
M=\(\dfrac{1}{x-1}-\dfrac{4}{x+1}+\dfrac{7x-1}{x^2-1}\)
a, Rút gọn M
b, Tính giá trị của M tại x = -3

\(a,M=\dfrac{x+1-4x+4+7x-1}{\left(x-1\right)\left(x+1\right)}=\dfrac{4\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{x-1}\\ b,x=-3\Rightarrow M=\dfrac{4}{-3-1}=-1\)
b.\(M=\dfrac{1}{-3-1}-\dfrac{4}{-3+1}+\dfrac{7\left(-3\right)-1}{\left(-3\right)^2-1}\)
\(M=\dfrac{-1}{4}-\left(-2\right)+\dfrac{11}{5}=3,95\)

a, \(M=\frac{3\left(x^2+1\right)}{\left(x^4+x^2\right)+\left(2x^3+2x\right)+\left(6x^2+6x\right)}=\frac{3\left(x^2+1\right)}{x^2\left(x^2+1\right)+2x\left(x^2+1\right)+6\left(x^2+1\right)}=\frac{3\left(x^2+1\right)}{\left(x^2+2x+6\right)\left(x^2+1\right)}=\frac{3}{x^2+2x+6}\)
b, ta có: \(M=\frac{3}{x^2+2x+6}=\frac{3}{\left(x^2+2x+1\right)+5}=\frac{3}{\left(x+1\right)^2+5}\)
Vì \(\left(x+1\right)^2\ge0\Rightarrow\left(x+1\right)^2+5\ge5\Rightarrow\frac{1}{\left(x+1\right)^2+5}\le\frac{1}{5}\Rightarrow M=\frac{3}{\left(x+1\right)^2+5}\le\frac{3}{5}\)
Dấu "=" xảy ra <=>x+1=0 <=> x=-1


`a)M=(x^4+2)/(x^6+1)+(x^2-1)/(x^4-x^2+1)-(x^2+3)/(x^4+4x^2+3)`
`=(x^4+2)/(x^6+1)+(x^2-1)/(x^4-x^2+1)-(x^2+3)/((x^2+1)(x^2+3))`
`=(x^4+2)/(x^6+1)+((x^2-1)(x^2+1))/(x^6+1)-1/(x^2+1)`
`=(x^4+2+x^4-1-x^4+x^2-1)/(x^2+1)`
`=(x^4+x^2)/(x^2+1)`
`=(x^2(x^2+1))/(x^2+1)`
`=x^2`
`b)` tìm gtnn chứ?
`M=x^2>=0`
Dấu '=" `<=>x=0`