Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(P=\left(1+2a\right)\left(1+2bc\right)\le\left(1+2a\right)\left(1+b^2+c^2\right)=\left(1+2a\right)\left(2-a^2\right)\)
\(=\frac{3}{2}\left(\frac{2}{3}+\frac{4}{3}a\right)\left(2-a^2\right)\le\frac{3}{8}\left(\frac{8}{3}+\frac{4}{3}a-a^2\right)^2=\frac{3}{8}\left[\frac{28}{9}-\left(a-\frac{2}{3}\right)^2\right]^2\)
\(\le\frac{3}{8}.\left(\frac{28}{9}\right)^2=\frac{98}{27}\)
Dấu \(=\)khi \(\hept{\begin{cases}b=c\\\frac{2}{3}+\frac{4}{3}a=2-a^2,a-\frac{2}{3}=0\\a^2+b^2+c^2=1\end{cases}}\Leftrightarrow\hept{\begin{cases}a=\frac{2}{3}\\b=c=\frac{\sqrt{\frac{5}{2}}}{3}\end{cases}}\).
Vậy \(maxP=\frac{98}{27}\).
Ta co : \(P=2a+2bc+2abc+1\)
Ap dung bdt Co-si : \(P\le a^2+b^2+c^2+2abc+2=2abc+3\)
Tiep tuc ap dung Co-si : \(1=a^2+b^2+c^2\ge3\sqrt[3]{a^2b^2c^2}< =>\sqrt[3]{a^2b^2c^2}\le\frac{1}{3}\)
\(< =>a^2b^2c^2\le\frac{1}{27}< =>abc\le\frac{1}{\sqrt{27}}\)
Khi do : \(2abc+3\le2.\frac{1}{\sqrt{27}}+3=\frac{2}{\sqrt{27}}+3\)
Suy ra \(P\le a^2+b^2+c^2+2abc+2\le\frac{2}{\sqrt{27}}+3\)
Dau "=" xay ra khi va chi khi \(a=b=c=\frac{1}{\sqrt{3}}\)
Vay Max P = \(\frac{2}{\sqrt{27}}+3\)khi a = b = c = \(\frac{1}{\sqrt{3}}\)
p/s : khong biet dau = co dung k nua , minh lam bay do
\(A=0.5\cdot4\sqrt{3-x}-\sqrt{3-x}-2\sqrt{3}+1=\sqrt{3-x}-2\sqrt{3}+1\) (xác định khi x=<3)
a)thay \(x=2\sqrt{2}\)vào a ra có
\(\sqrt{3-2\sqrt{2}}-2\sqrt{3}+1=\sqrt{\left(\sqrt{2}-1\right)^2}-2\sqrt{3}+1\)
\(=\sqrt{2}-1+2\sqrt{3}+1=\sqrt{2}+2\sqrt{3}\)
Để A=1<=> \(\sqrt{3-x}-2\sqrt{3}+1=1\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}+1-1=0\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}=0\\ \Leftrightarrow3-x=12\Leftrightarrow x=-9\)
a, Gọi I là trung điểm AB
Xét tam giác AEB vuông tại E, I là trung điểm
=> \(EI=AI=IB=\frac{AB}{2}\)(1)
Xét tam giác ADB vuông tại D, I là trung điểm
=> \(DI=AI=IB=\frac{AB}{2}\)(2)
Từ (1) ; (2) => A ; D ; B ; F cùng nằm trên đường tròn (I;AB/2)
b, Gọi O là trung điểm AC
Xét tam giác AFC vuông tại F, O là trung điểm
=> \(FO=AO=CO=\frac{AC}{2}\)(3)
Xét tam giác CDA vuông tại D, O là trung điểm
=> \(DO=AO=CO=\frac{AC}{2}\)(4)
Từ (3) ; (4) => A ; D ; C ; F cùng nằm trên đường tròn (O;AC/2)
c, Gọi T là trung điểm BC
Xét tam giác BFC vuông tại F, T là trung điểm
=> \(FT=BT=CT=\frac{BC}{2}\)(5)
Xét tam giác BEC vuông tại E, T là trung điểm
=> \(ET=BT=CT=\frac{BC}{2}\)(6)
Từ (5) ; (6) => B ; C ; E ; F cùng nằm trên đường tròn (T;BC/2)
\(3\times y^2-12\times y+12\times\)
\(=3\times\cdot\left(y^2-4y+4\right)\)
\(=3\times\cdot\left(y^2-2\cdot2y+2^2\right)\)
\(=3\times\cdot\left(y-2\right)^2\)
\(3xy^2-12xy+12x\)
\(=3x\left(y^2-4y+4\right)\)
\(=3x\left(y-2\right)^2\)
\(=\left(sin^2\alpha\right)^3+\left(cos^2\alpha\right)^3+3sin^2\alpha-cos^2\alpha\)
\(=\left(sin^2\alpha+cos^2\alpha\right)\left(sin^4\alpha-sin^2\alpha.cos^2\alpha+cos^4\alpha\right)+3sin^2\alpha-cos^2\alpha\)
\(=sin^4\alpha-sin^2\alpha.cos^2\alpha+cos^4\alpha+3sin^2\alpha-cos^2\alpha\)
\(=sin^4\alpha+cos^4\alpha-sin^2\alpha.cos^2\alpha+3sin^2\alpha-cos^2\alpha\)
\(=\left(sin^2\alpha\right)^2+\left(cos^2\right)^2-sin^2\alpha.cos^2\alpha+3sin^2\alpha-cos^2\)
\(=1-2sin^2\alpha.cos^2\alpha-sin^2\alpha.cos^2\alpha+3sin^2\alpha-cos^2\alpha\)
\(=1-3sin^2\alpha.cos^2\alpha+3sin^2\alpha.cos^2\alpha-cos^2\alpha\)
\(=1-3sin^2\alpha.\left(1-sin^2\alpha\right)+3sin^2\alpha-\left(1-sin^2\alpha\right)\)
\(=1-3sin^2\alpha-sin^2\alpha+3sin^2\alpha-\left(1-sin^2\alpha\right)\)
\(1-3sin^2\alpha-sin^2\alpha+3sin^2\alpha-1+sin^2\alpha\)
\(=0\)
đề : Cho đoạn thẳng AB cùng điểm C thuộc đoạn thẳng đó (C khác A và B). Về cùng một nửa mặt phẳng bờ AB, kẻ hai tia Ax và By cùng vuông góc với AB. Trên tia Ax lấy điểm M cố định. Kẻ tia Cz vuông góc với tia CM tại C, tia Cz cắt tia By tại K. Vẽ đường tròn tâm O đường kính MC cắt MK tại E
a)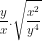
= 
.
= 
.
= 
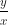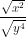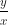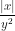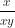vì x > 0.
Do đó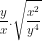
= 
.
b)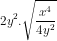
= 
.
= 
.
.
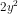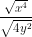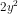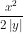Vì y < 0 nên │y│= -y. Do đó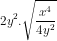
= 
.
= 
.
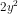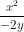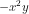c) 5xy.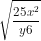
= 5xy.
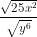= 5xy.
.
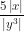Vì x < 0, y > 0 nên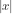
= -x và 
= 
.
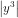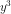Do đó: 5xy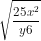
= 5xy.
= -
.
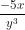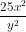d) 0,2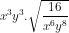
= 
= 0,2
= 
Nếu x > 0 thì
> 0 nên 
. Do đó 0,2
= 
.
Nếu x < 0 thì
< 0 nên 
. Do đó 0,2
= -
.
a)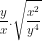
= 
.
= 
.
= 
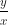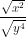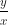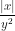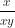vì x > 0.
Do đó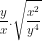
= 
.
b)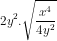
= 
.
= 
.
.
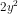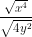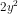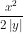Vì y < 0 nên │y│= -y. Do đó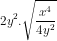
= 
.
= 
.
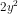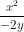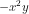c) 5xy.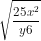
= 5xy.
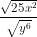= 5xy.
.
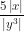Vì x < 0, y > 0 nên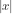
= -x và 
= 
.
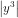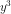Do đó: 5xy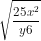
= 5xy.
= -
.
d) 0,2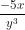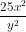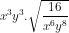
= 
= 0,2
= 
Nếu x > 0 thì
> 0 nên 
. Do đó 0,2
= 
.
Nếu x < 0 thì
< 0 nên 
. Do đó 0,2
= -
.