Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
\(A=\left(a-4\right)\left(a+5\right)-\left(a-5\right)\left(a+4\right)\)
\(=\left[\left(a-4\right)a+5\left(a-4\right)\right]-\left[\left(a-5\right)a+4\left(a-5\right)\right]\)
\(=\left[a^2-4a+5a-20\right]-\left[a^2-5a+4a-20\right]\)
\(=a^2-4a+5a-20-a^2+5a-4a+20\)
\(=\left(a^2-a^2\right)+\left(-4a+5a+5a-4a\right)+\left(-20+20\right)\)
\(=0+2a+0\)
\(=2a\)
b) Ta có:
\(B=\left(2-a\right)\left(a+7\right)-\left(a-1\right)\left(a+2\right)\)
\(=\left[\left(2-a\right)a+7\left(2-a\right)\right]-\left[\left(a-1\right)a+2\left(a-1\right)\right]\)
\(=\left[2a-a^2+14-7a\right]-\left[a^2-a+2a-2\right]\)
\(=2a-a^2+14-7a-a^2+a-2a+2\)
\(=\left(2a-7a+a-2a\right)-\left(a^2+a^2\right)+\left(14+2\right)\)
\(=-6a-2a^2+16\)

Có đầy câu hỏi tương tự đáy bạn lên các câu hỏi đó mà xem

a: \(A=\dfrac{a^3+a^2+a^2+a-a-1}{\left(a+1\right)\left(a^2-a+1\right)+2a\left(a+1\right)}\)
\(=\dfrac{\left(a+1\right)\left(a^2+a-1\right)}{\left(a+1\right)\left(a^2+a+1\right)}=\dfrac{a^2+a-1}{a^2+a+1}\)
b: Nếu a là số nguyên âm thì a<0
Vì a2+a=a(a+1) chia hết cho 2 nên \(a^2+a-1;a^2+a+1\) là hai số tự nhiên lẻ liên tiếp
hay A là phân số tối giản

a) A=x^2+2
b) mình nghĩ x thuộc tập hợp R
c)GTNN của A=1/4 khi x=1/2

\(A=\left(\frac{1-\left(\sqrt{a}\right)^3}{1-\sqrt{a}}\right)\left(\frac{1-\sqrt{a}}{1-\left(\sqrt{a}\right)^2}\right)^2\)
\(=\left(1+\sqrt{a}+a\right).\frac{1}{\left(1+\sqrt{a}\right)^2}\)
\(=\frac{1+\sqrt{a}+a}{1+2\sqrt{a}+a}\)

ta có:
\(log^{\left(2a^2\right)}_2+\left(log_2^a\right)a^{log_a^{\left(log^a_1+1\right)}}+\frac{1}{2}log^2_2a^4=log_2^2+log_2^{a^2}+log_2^a\left(log^a_2+1\right)+\frac{1}{2}log^2_2a^4\)
\(=1+2log^a_2+log^a_2\left(1+log^a_2\right)+2log^2a_2\)
\(=3log^2_2a+3log^a_2+1\)
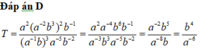

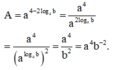
Đáp án B
Ta có
P = a . a 2 . 1 a 4 3 : a 7 24 = a . a 2 . a 1 4 3 : a 7 24 = a . a 7 4 1 3 : a 7 24 = a 19 12 1 2 : a 7 24 = a 1 2 .