Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi v = 120 km/h
⇔ 3t2 – 30t + 135 = 120
⇔ 3t2 – 30t + 15 = 0
Có a = 3; b’ = -15; c = 15; Δ’ = b’2 – ac = (-15)2 – 3.15 = 180
Phương trình có hai nghiệm phân biệt
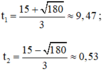
Vì rada quan sát chuyển động của ô tô trong 10 phút nên t1 và t2 đều thỏa mãn.
Vậy tại t = 9,47 phút hoặc t = 0,53 phút thì vận tốc ô tô bằng 120km/h.

a) Khi t = 5 (phút) thì v = 3 . 52 – 30 . 5 + 135 = 60 (km/h)
b) Khi v = 120 (km/h), để tìm t ta giải phương trình 120 = 3t2 – 30t + 135
Hay t2 – 10t + 5 = 0. Có a = 1, b = -10, b’ = -5, c = 5.
∆’ = 52 – 5 = 25 – 5 = 20, √∆’ = 2√5
t1 = 5 + 2√5 ≈ 9,47, t2 = 5 - 2√5 ≈ 0,53
Vì rađa chỉ theo dõi trong 10 phút nên 0 < t < 10 nên cả hai giá trị của t đều thích hợp. Vậy t1 ≈ 9,47 (phút), t2 ≈ 0,53 (phút).
a) Khi t = 5 (phút) thì v = 3 . 52 – 30 . 5 + 135 = 60 (km/h)
b) Khi v = 120 (km/h), để tìm t ta giải phương trình 120 = 3t2 – 30t + 135
Hay t2 – 10t + 5 = 0. Có a = 1, b = -10, b’ = -5, c = 5.
∆’ = 52 – 5 = 25 – 5 = 20, √∆’ = 2√5
t1 = 5 + 2√5 ≈ 9,47, t2 = 5 - 2√5 ≈ 0,53
Vì rađa chỉ theo dõi trong 10 phút nên 0 < t < 10 nên cả hai giá trị của t đều thích hợp. Vậy t1 ≈ 9,47 (phút), t2 ≈ 0,53 (phút).

mọi người ơi giúp mình với ![]() nagyf mai là hạn chót nộp bài r
nagyf mai là hạn chót nộp bài r

Bài 24:
Gọi x(km/h) và y(h) lần lượt là vận tốc và thời gian ô tô ban đầu dự định đi từ A đến B(Điều kiện: x>0; y>0)
Độ dài quãng đường AB là: xy(km)
Vì khi vận tốc ô tô tăng thêm 10km/h thì đến B sớm hơn 30 phút so với dự định nên ta có phương trình:
\(\left(x+10\right)\left(y-\dfrac{1}{2}\right)=xy\)
\(\Leftrightarrow xy-\dfrac{1}{2}x+10y-5=xy\)
\(\Leftrightarrow xy-\dfrac{1}{2}x+10y-5-xy=0\)
\(\Leftrightarrow\dfrac{-1}{2}x+10y=5\)(1)
Vì khi vận tốc ô tô giảm đi 5km/h thì đến B muộn 20 phút so với dự định nên ta có phương trình:
\(\left(x-5\right)\left(y+\dfrac{1}{3}\right)=xy\)
\(\Leftrightarrow xy+\dfrac{1}{3}x-5y-\dfrac{5}{3}=xy\)
\(\Leftrightarrow xy+\dfrac{1}{3}x-5y-\dfrac{5}{3}-xy=0\)
\(\Leftrightarrow\dfrac{1}{3}x-5y=\dfrac{5}{3}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{-1}{2}x+10y=5\\\dfrac{1}{3}x-5y=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-1}{6}x+\dfrac{10}{3}y=\dfrac{5}{3}\\\dfrac{1}{6}x-\dfrac{5}{2}y=\dfrac{5}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{6}y=\dfrac{5}{6}\\\dfrac{1}{3}x-5y=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\\dfrac{1}{3}x=\dfrac{5}{3}+5y=\dfrac{5}{3}+5=\dfrac{20}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=20\\y=1\end{matrix}\right.\)(thỏa ĐK)
Độ dài quãng đường AB là:
\(xy=20\cdot1=20\left(km\right)\)
Vậy: Quãng đường AB dài 20km
Bài 25:
Gọi vận tốc xe đi từ A và xe đi từ B lần lượt là a, b(km/h; a>10; b>0; a>b)
Mỗi giờ xe đi từ A đi nhanh hơn xe kia 10km => a - b = 10 (1)
Sau 5 giờ xe đi từ A đi được: 5a (km)
Sau 5 giờ xe đi từ B đi được: 5b (km)
Nếu đi ngược chiều, 2 xe gặp nhau sau 5 giờ nên ta có: 5a+5b=350 (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{{}\begin{matrix}a-b=10\\5a+5b=350\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}5a-5b=50\\5a+5b=350\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}10a=400\\a-b=10\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}a=40\\b=30\end{matrix}\right.\) (tm)
Vậy vận tốc của xe đi từ A và xe đi từ B lần lượt là 40km/h và 30km/h

tôi học lớp 6 không biết giải phương trình ,nhưng cũng chỉ học qua phương trình bậc nhất thôi! thông cảm ha!

Bài 27:
Gọi x(km/h) và y(h) lần lượt là vận tốc và thời gian mà ô tô dự định ban đầu(Điều kiện: x>0; y>0)
Độ dài quãng đường đi từ Hà Nội đến Thanh Hóa là:
xy(km)
Vì khi vận tốc ô giảm 10km/h thì thời gian tăng 45 phút nên ta có phương trình:
\(\left(x-10\right)\left(y+\dfrac{3}{4}\right)=xy\)
\(\Leftrightarrow xy+\dfrac{3}{4}x-10y-\dfrac{15}{2}=xy\)
\(\Leftrightarrow\dfrac{3}{4}x-10y=\dfrac{15}{2}\)(1)
Vì khi vận tốc ô tô tăng 10km/h thì thời gian giảm 30 phút nên ta có phương trình:
\(\left(x+10\right)\left(y-\dfrac{1}{2}\right)=xy\)
\(\Leftrightarrow xy-\dfrac{1}{2}x+10y-5=xy\)
\(\Leftrightarrow\dfrac{-1}{2}x+10y=5\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{3}{4}x-10y=\dfrac{15}{2}\\\dfrac{-1}{2}x+10y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{4}x=\dfrac{25}{2}\\\dfrac{-1}{2}x+10y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{25}{2}:\dfrac{1}{4}=\dfrac{25}{2}\cdot4=50\\10y-25=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=50\\10y=30\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=50\\y=3\end{matrix}\right.\)(thỏa ĐK)
Vậy: Vận tốc đã định của ô tô là 50km/h
Thời gian đã định của ô tô là 3h
Quãng đường Hà Nội-Thanh Hóa dài 150km
a) Tại t = 5, ta có: v = 3 . 5 2 – 30 . 5 + 135 = 60 ( k m / h )
b) Khi v = 120 km/h
⇔ 3 t 2 – 30 t + 135 = 120 ⇔ 3 t 2 – 30 t + 15 = 0
Có a = 3; b’ = -15; c = 15; Δ ’ = b ’ 2 – a c = ( - 15 ) 2 – 3 . 15 = 180
Phương trình có hai nghiệm phân biệt
Vì rada quan sát chuyển động của ô tô trong 10 phút nên t 1 v à t 2 đều thỏa mãn.
Vậy tại t = 9,47 phút hoặc t = 0,53 phút thì vận tốc ô tô bằng 120km/h.