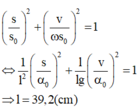Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng thời gian gia tốc và vận tốc cùng chiều là khoảng thời gian vật đi từ vị trí biên đến vị trí cân bằng tức t=T/4
T=0.05π.4=0,2π(s)→ω=10rad/s→Δl=g/ω2=10cm
Mà khoảng lò xo nén trong 1 chu kì là t=T/4 thì lò xo không bị biến dạng ở vị trí x= - A/√2 (quy ước chiều dương hướng xuống dưới)
→A=√2.Δl=10√2 cm
Suy ra: vmax=A.ω=√2(m/s)
Chọn đáp án B.

Áp dụng công thức:
\(g=g_0.\dfrac{R^2}{(R+h)^2}\)
Trong đó, \(g_0\) là gia tốc trọng trường ở mặt đất.
$R$ là bán kính trái đất.
$h$ là độ cao của vật.

Đáp án B
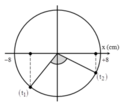
Hướng dẫn:
+ Tốc độ của vật sau khoảng thời gian t = 0,11 s rơi tự do là v 0 = g t = 10.0 , 11 = 1 , 1 m / s
+ Sau khi điểm chính giữa của lò xo được giữ cố định thì phần lò xo tham gia vào dao động có độ cứng k = 2 k 0 = 25 cm.
→ Tần số góc của dao động ω = k m = 25 0 , 1 = 5 π rad/s → T = 0,4 s.
+ Độ biến dạng của lò xo khi vật đi qua vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 25 = 4 c m
+ Biên độ dao động của con lắc A = Δ l 0 2 + v 0 ω 2 2 = 4 2 + 110 5 π 2 = 8 cm.
+ Tại t 1 = 0 , 11 s vật đang ở vị trí có li độ x = − Δ l 0 = − A 2 = − 4 c m sau khoảng thời gian Δ t = t 2 – t 1 = 0 , 25 T = 0 , 1 s vật đến vị trí có li độ x = 3 2 A , tốc độ của vật khi đó v = 1 2 v m a x = 1 2 ω A = 1 2 .5 π .8 = 20 π cm/s

Đáp án B
Phương pháp: Sử dụng lí thuyết về con lắc lò xo dao động điều hòa theo phương thẳng đứng
Cách giải:
+ Tần số góc ω = 2 π T
+ Độ giãn của lò xo ở VTCB:
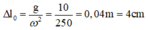
+ Do ∆ l 0 < A nên lực đàn hồi của lò xo có độ lớn cực tiểu bằng 0 tại vị trí lò xo không biến dạng
=> Thời gian vật đi từ VTCB (x = 0) đến VT lò xo không biến dạng (x = -4 cm) là t = T/12 = 1/30 s
=> Chọn B

Câu hỏi này bạn cần biết phân tích chuyển động biến đổi đều của xe, quãng đường xe chuyển động và âm chuyển động để giải bài toán.
+ Biết mức cường độ âm tại N lớn hơn mức cường độ âm tại M là 20 dB, ta có:
\({{L}_{N}}-{{L}_{M}}=10.\lg{{\left( \dfrac{{{R}_{M}}}{{{R}_{N}}} \right)}^{2}}=20\Rightarrow {{R}_{M}}=OM=10{{R}_{N}}=100m\)
\(\Rightarrow MN = OM – ON = 90 m\)
Vật (thiết bị) đi từ M nhanh dần đều đến trung điểm của MN, sau đó chuyển động chậm dần và dừng lại tại N, nên ta có: \({{t}_{MN}}=2.{{t}_{MC}}\)(C là trung điểm của MN)
\(MC=\dfrac{MN}{2}=\dfrac{1}{2}at_{MC}^{2}\Rightarrow {{t}_{MC}}=\sqrt{\dfrac{MN}{a}}\)
\(\Rightarrow t={{t}_{MN}}=2\sqrt{\dfrac{MN}{a}}=2\sqrt{\dfrac{90}{04}}=30s\)
Vậy giá trị gần nhất là 32s